
分析 (1)將已知等式兩邊平方,利用三角函數的平方關系式,直接求出sinxcosx的值;
(2)由角的范圍可求sinx-cosx<0,由(1)結論即可計算得解;
(3)化簡所求,利用(1)(2)的結論即可計算得解.
解答 解:(1)將sinx+cosx=$\frac{1}{5}$,兩邊平方得:(sinx+cosx)2=1+2sinxcosx=$\frac{1}{25}$,
故可得:sinxcosx=-$\frac{12}{25}$.
(2)因為:-$\frac{π}{2}$<x<0,可得:sinx<0,cosx>0,sinx-cosx<0,
又因為:(sinx-cosx)2=1-2sinxcosx=1-(-$\frac{24}{25}$)=$\frac{49}{25}$,
所以:sinx-cosx=-$\frac{7}{5}$.
(3)$\frac{1}{co{s}^{2}x-si{n}^{2}x}$=$\frac{1}{(cosx-sinx)(cosx+sinx)}$=$\frac{1}{\frac{7}{5}×\frac{1}{5}}$=$\frac{25}{7}$.
點評 本題考查同角三角函數的基本關系式的應用,三角函數的化簡求值,考查了計算能力,屬于中檔題.


 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如表是一個由n2個正數組成的數表,用aij表示第i行第j個數(i,j∈N),已知數表中第一列各數從上到下依次構成等差數列,每一行各數從左到右依次構成等比數列,且公比都相等.已知a11=1,a31+a61=9,a35=48.
如表是一個由n2個正數組成的數表,用aij表示第i行第j個數(i,j∈N),已知數表中第一列各數從上到下依次構成等差數列,每一行各數從左到右依次構成等比數列,且公比都相等.已知a11=1,a31+a61=9,a35=48.查看答案和解析>>
科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(理)試卷(解析版) 題型:解答題
市場上有一種新型的強力洗衣粉,特點是去污速度快,已知每投放 (
(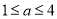 且
且 )個單位的洗衣粉液在一定量水的洗衣機中,它在水中釋放的濃度
)個單位的洗衣粉液在一定量水的洗衣機中,它在水中釋放的濃度 (克/升)隨著時間
(克/升)隨著時間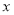 (分鐘)變化的函數關系式近似為
(分鐘)變化的函數關系式近似為 ,其中
,其中 ,若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和,根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起有效去污的作用.
,若多次投放,則某一時刻水中的洗衣液濃度為每次投放的洗衣液在相應時刻所釋放的濃度之和,根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起有效去污的作用.
(1)若只投放一次4個單位的洗衣液,則有效去污時間可能達幾分鐘?
(2)若先投放2個單位的洗衣液,6分鐘后投放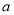 個單位的洗衣液,要使接下來的4分鐘中能夠持續有效去污,試求
個單位的洗衣液,要使接下來的4分鐘中能夠持續有效去污,試求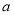 的最小值(精確到0.1,參考數據:
的最小值(精確到0.1,參考數據: 取
取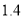 ).
).
查看答案和解析>>
科目:高中數學 來源:2016-2017學年河北正定中學高二上月考一數學(文)試卷(解析版) 題型:選擇題
運行下面的程序,若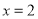 ,則輸出的
,則輸出的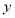 等于( )
等于( )

A.9 B.7 C.13 D.11
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com