
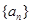 是等差數(shù)列,
是等差數(shù)列,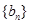 是公比為
是公比為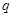 的等比數(shù)列,
的等比數(shù)列,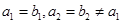 ,記
,記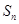 為數(shù)列
為數(shù)列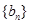 的前
的前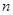 項(xiàng)和,
項(xiàng)和,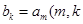 是大于
是大于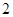 的正整數(shù)
的正整數(shù)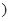 ,求證:
,求證: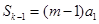 ;
;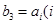 是某一正整數(shù)
是某一正整數(shù)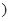 ,求證:
,求證: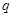 是整數(shù),且數(shù)列
是整數(shù),且數(shù)列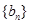 中每一項(xiàng)都是數(shù)列
中每一項(xiàng)都是數(shù)列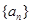 中的項(xiàng);
中的項(xiàng);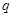 ,使等比數(shù)列
,使等比數(shù)列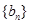 中有三項(xiàng)成等差數(shù)列?若存在,寫出一個(gè)
中有三項(xiàng)成等差數(shù)列?若存在,寫出一個(gè)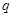 的值,并加以說明;若不存在,請(qǐng)說明理由;
的值,并加以說明;若不存在,請(qǐng)說明理由;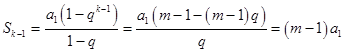
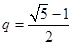 使得
使得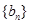 中有三項(xiàng)
中有三項(xiàng)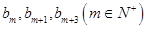 成等差數(shù)列。
成等差數(shù)列。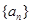 的公差為
的公差為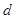 ,由
,由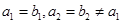 ,知
,知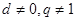 ,
,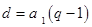 (
(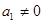 )
)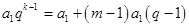 ,
,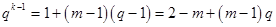 ,
,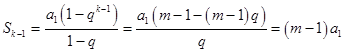
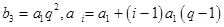 ,由
,由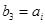 ,
,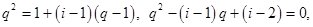 解得,
解得,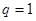 或
或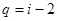 ,但
,但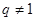 ,所以
,所以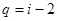 ,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353825251.png" style="vertical-align:middle;" />是正整數(shù),所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353825251.png" style="vertical-align:middle;" />是正整數(shù),所以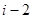 是整數(shù),即
是整數(shù),即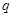 是整數(shù),設(shè)數(shù)列
是整數(shù),設(shè)數(shù)列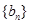 中任意一項(xiàng)為
中任意一項(xiàng)為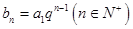 ,設(shè)數(shù)列
,設(shè)數(shù)列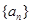 中的某一項(xiàng)
中的某一項(xiàng)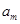
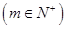 =
=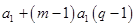
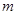 ,使得
,使得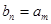 ,即在方程
,即在方程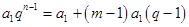 中
中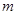 有正整數(shù)解即可,
有正整數(shù)解即可,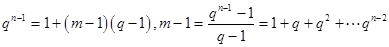 ,所以
,所以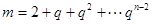 ,若
,若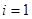 ,則
,則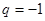 ,那么
,那么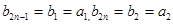 ,當(dāng)
,當(dāng)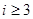 時(shí),因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004354200593.png" style="vertical-align:middle;" />,只要考慮
時(shí),因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004354200593.png" style="vertical-align:middle;" />,只要考慮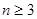 的情況,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353700487.png" style="vertical-align:middle;" />,所以
的情況,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353700487.png" style="vertical-align:middle;" />,所以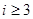 ,因此
,因此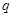 是正整數(shù),所以
是正整數(shù),所以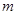 是正整數(shù),因此數(shù)列
是正整數(shù),因此數(shù)列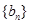 中任意一項(xiàng)為
中任意一項(xiàng)為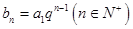 與數(shù)列
與數(shù)列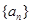 的第
的第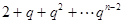 項(xiàng)相等,從而結(jié)論成立。
項(xiàng)相等,從而結(jié)論成立。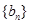 中有三項(xiàng)
中有三項(xiàng)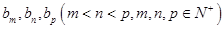 成等差數(shù)列,則有
成等差數(shù)列,則有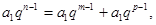 設(shè)
設(shè)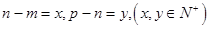 ,所以2
,所以2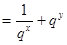 ,令
,令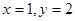 ,則
,則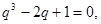
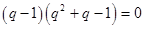 ,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353763375.png" style="vertical-align:middle;" />,所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824004353763375.png" style="vertical-align:middle;" />,所以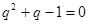 ,所以
,所以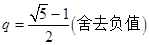 ,即存在
,即存在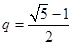 使得
使得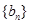 中有三項(xiàng)
中有三項(xiàng)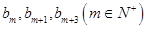 成等差數(shù)列。
成等差數(shù)列。

 第三學(xué)期贏在暑假系列答案
第三學(xué)期贏在暑假系列答案 學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車道快樂假期暑假作業(yè)新疆人民出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
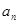 }中,
}中,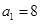 ,
,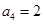 ,且滿足
,且滿足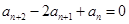
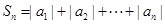 ,求
,求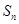 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
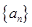 是等差數(shù)列,其中
是等差數(shù)列,其中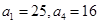 ]
]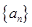 的通項(xiàng);
的通項(xiàng); 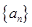 從哪一項(xiàng)開始小于0;
從哪一項(xiàng)開始小于0;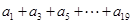 值。]
值。]查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
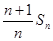
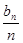 的最小值.
的最小值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
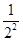 +
+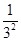 +…+
+…+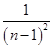 ] (n≥2,n∈N)
] (n≥2,n∈N)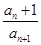 =
=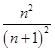
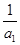 )(1+
)(1+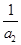 )…(1+
)…(1+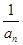 )<4
)<4查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
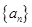 的各項(xiàng)均為正數(shù),前
的各項(xiàng)均為正數(shù),前 項(xiàng)和為
項(xiàng)和為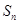 ,對(duì)于任意的
,對(duì)于任意的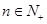 ,
,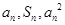 成等差數(shù)列,設(shè)數(shù)列
成等差數(shù)列,設(shè)數(shù)列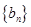 的前
的前 項(xiàng)和為
項(xiàng)和為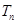 ,且
,且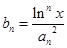 ,則對(duì)任意的實(shí)數(shù)
,則對(duì)任意的實(shí)數(shù)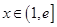 (
(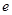 是自然對(duì)數(shù)的底)和任意正整數(shù)
是自然對(duì)數(shù)的底)和任意正整數(shù) ,
,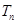 小于的最小正整數(shù)為( )
小于的最小正整數(shù)為( )A.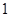 | B.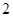 | C.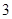 | D.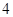 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com