
分析 根據數量積坐標的運算求解f(x)化簡為y=Asin(ωx+φ)的形式,再利用周期公式求函數的最小正周期,將內層函數看作整體,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;
解答 解:向量$\overrightarrow{a}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{b}$=(cos x,sin x).
那么:函數f (x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx=sin(x+$\frac{π}{3}$)
函數的最小正周期T$\frac{2π}{ω}=\frac{2π}{1}=2π$.
令$2kπ-\frac{π}{2}$≤x+$\frac{π}{3}$≤2k$π+\frac{π}{2}$,(k∈Z)
解得:$2kπ-\frac{5π}{6}$≤x≤2kπ$+\frac{π}{6}$,
故得函數f(x)的單調遞增區間為[$2kπ-\frac{5π}{6}$,2kπ$+\frac{π}{6}$],(k∈Z)
點評 本題考查了三角函數的恒等式變換應用.數量積坐標的表達,復合函數的單調性.屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-2,-1) | B. | (-∞,-2] | C. | [-2,-1)∪(3,+∞) | D. | (-2,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
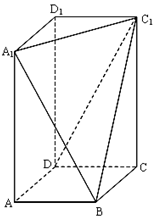 已知長方體ABCD-A1B1C1D1,其中AB=BC=2,過A1、C1、B三點的平面截去長方體的一個角后.得到如圖所示的,且這個幾何體的體積為$\frac{40}{3}$.
已知長方體ABCD-A1B1C1D1,其中AB=BC=2,過A1、C1、B三點的平面截去長方體的一個角后.得到如圖所示的,且這個幾何體的體積為$\frac{40}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
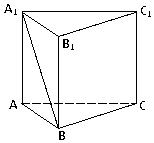 如圖,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如圖,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com