
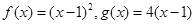 ,數列
,數列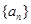 滿足
滿足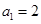 ,且
,且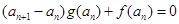 .
.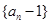 是否是等比數列?(5分)
是否是等比數列?(5分)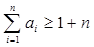 .(5分)
.(5分)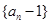 是首項為
是首項為 ,公比為
,公比為 的等比數列. (2)證明:見解析。
的等比數列. (2)證明:見解析。 是首項為1,公比為
是首項為1,公比為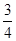 的等比數列
的等比數列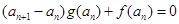 得
得 ,即
,即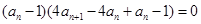 ----------1分
----------1分 或
或 ∵
∵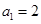 ,∴
,∴ 不合舍去.
不合舍去. 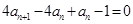 得
得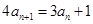 ,
, ,(
,( )--------3分
)--------3分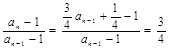 ,
,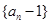 是首項為
是首項為 ,公比為
,公比為 的等比數列. -------------------5分
的等比數列. -------------------5分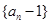 是首項為
是首項為 ,公比為
,公比為 的等比數列
的等比數列 ,∴
,∴ , ------------------6分
, ------------------6分 =
=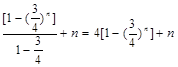 ---8分
---8分 有
有 ,
, ,∴
,∴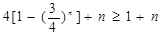 ,即
,即 ---10分
---10分

 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com