
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() ,
,![]() ,試證:
,試證:![]() .
.
【答案】(1)單調增區間為![]() 與
與![]() ,減區間為
,減區間為![]() ;(2)見解析
;(2)見解析
【解析】
(1)求導,令![]() ,可得增區間,令
,可得增區間,令![]() ,可得減區間,要注意函數定義域為
,可得減區間,要注意函數定義域為![]() ;
;
(2)構造函數![]() ,
,![]() ,求導后得,
,求導后得,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上單調遞增,利用函數的單調性可得
上單調遞增,利用函數的單調性可得![]() 在
在![]() 上恒成立,因為
上恒成立,因為![]() ,所以
,所以![]() ,即
,即![]() ①;同理,構造函數
①;同理,構造函數![]() ,
,![]() ,可證
,可證![]() ②,結合①②,結論可證.
②,結合①②,結論可證.
(1)由題設知函數![]() 的定義域為
的定義域為![]() 且
且![]()
故當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
所以![]() 的單調增區間為
的單調增區間為![]() 與
與![]() ,減區間為
,減區間為![]() ;
;
(2)由(1)知:![]() ,先證
,先證![]() .
.
構造函數![]() ,
,![]()
則![]()
故![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上單調遞增
上單調遞增
所以![]() 在
在![]() 上恒成立,
上恒成立,
又![]() ,得
,得![]() ,又
,又![]() 且函數
且函數![]() 在
在![]() 上單調遞減
上單調遞減
故![]() ,即
,即![]() ①
①
再證![]() .構造函數
.構造函數![]() ,
,![]()
![]()
故![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上單調遞增
上單調遞增
所以![]() 在
在![]() 上恒成立,
上恒成立,
又![]() ,得
,得![]() ,
,
又![]() 且函數
且函數![]() 在
在![]() 上單調遞增
上單調遞增
故![]() ,即
,即![]() ②
②
結合①②得:![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】“移動支付、高鐵、網購、共享單車”被稱為中國的“新四大發明”.為了幫助50歲以上的中老年人更快地適應“移動支付”,某機構通過網絡組織50歲以上的中老年人學習移動支付相關知識.學習結束后,每人都進行限時答卷,得分都在![]() 內.在這些答卷(有大量答卷)中,隨機抽出
內.在這些答卷(有大量答卷)中,隨機抽出![]() 份,統計得分繪出頻率分布直方圖如圖.
份,統計得分繪出頻率分布直方圖如圖.
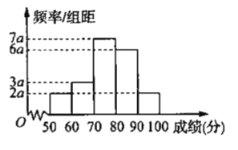
(1)求出圖中![]() 的值,并求樣本中,答卷成績在
的值,并求樣本中,答卷成績在![]() 上的人數;
上的人數;
(2)以樣本的頻率為概率,從參加這次答卷的人群中,隨機抽取![]() 名,記成績在
名,記成績在![]() 分以上(含
分以上(含![]() 分)的人數為
分)的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著科學技術的飛速發展,網絡也已經逐漸融入了人們的日常生活,網購作為一種新的消費方式,因其具有快捷、商品種類齊全、性價比高等優勢而深受廣大消費者認可.某網購公司統計了近五年在本公司網購的人數,得到如下的相關數據(其中“x=1”表示2015年,“x=2”表示2016年,依次類推;y表示人數):
x | 1 | 2 | 3 | 4 | 5 |
y(萬人) | 20 | 50 | 100 | 150 | 180 |
(1)試根據表中的數據,求出y關于x的線性回歸方程,并預測到哪一年該公司的網購人數能超過300萬人;
(2)該公司為了吸引網購者,特別推出“玩網絡游戲,送免費購物券”活動,網購者可根據拋擲骰子的結果,操控微型遙控車在方格圖上行進. 若遙控車最終停在“勝利大本營”,則網購者可獲得免費購物券500元;若遙控車最終停在“失敗大本營”,則網購者可獲得免費購物券200元. 已知骰子出現奇數與偶數的概率都是![]() ,方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,網購者每拋擲一次骰子,遙控車向前移動一次.若擲出奇數,遙控車向前移動一格(從
,方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,網購者每拋擲一次骰子,遙控車向前移動一次.若擲出奇數,遙控車向前移動一格(從![]() 到
到![]() )若擲出偶數遙控車向前移動兩格(從
)若擲出偶數遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第
),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第![]() 格的概率為
格的概率為![]() ,試證明
,試證明![]() 是等比數列,并求網購者參與游戲一次獲得免費購物券金額的期望值.
是等比數列,并求網購者參與游戲一次獲得免費購物券金額的期望值.
附:在線性回歸方程![]() 中,
中,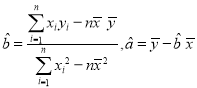 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年1月6日,中國物流與采購聯合會正式發布了中國倉儲指數,中國倉儲指數是反映倉儲行業經營和國內市場主要商品供求狀況與變化趨勢的一套指數體系,如圖所示的折線圖是2019年甲企業和乙企業的倉儲指數走勢情況.根據該折線圖,下列結論中不正確的是( )
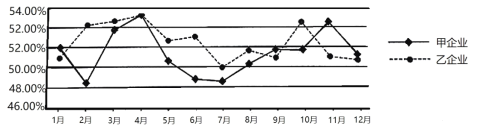
A.2019年1月至4月甲企業的倉儲指數比乙企業的倉儲指數波動大
B.甲企業2019年的年平均倉儲指數明顯低于乙企業2019年的年平均倉儲指數
C.兩企業2019年的最大倉儲指數都出現在4月份
D.2019年7月至9月乙企業的倉儲指數的增幅高于甲企業
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是定義在
是定義在![]() 上的函數,若對任何實數
上的函數,若對任何實數![]() 以及
以及![]() 中的任意兩數
中的任意兩數![]() 、
、![]() ,恒有
,恒有![]() ,則稱
,則稱![]() 為定義在
為定義在![]() 上的
上的![]() 函數.
函數.
(1)證明函數![]() 是定義域上的
是定義域上的![]() 函數;
函數;
(2)判斷函數![]() 是否為定義域上的
是否為定義域上的![]() 函數,請說明理由;
函數,請說明理由;
(3)若![]() 是定義域為
是定義域為![]() 的函數,且最小正周期為
的函數,且最小正周期為![]() ,試證明
,試證明![]() 不是
不是![]() 上的
上的![]() 函數.
函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】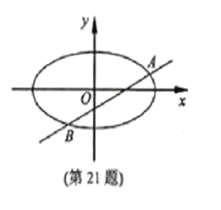
(本題滿分15分)已知m>1,直線![]() ,
,
橢圓![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點.
的左、右焦點.
(Ⅰ)當直線![]() 過右焦點
過右焦點![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() ,
,
![]() 的重心分別為
的重心分別為![]() .若原點
.若原點![]() 在以線段
在以線段
![]() 為直徑的圓內,求實數
為直徑的圓內,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com