
【題目】隨著科學技術的飛速發展,網絡也已經逐漸融入了人們的日常生活,網購作為一種新的消費方式,因其具有快捷、商品種類齊全、性價比高等優勢而深受廣大消費者認可.某網購公司統計了近五年在本公司網購的人數,得到如下的相關數據(其中“x=1”表示2015年,“x=2”表示2016年,依次類推;y表示人數):
x | 1 | 2 | 3 | 4 | 5 |
y(萬人) | 20 | 50 | 100 | 150 | 180 |
(1)試根據表中的數據,求出y關于x的線性回歸方程,并預測到哪一年該公司的網購人數能超過300萬人;
(2)該公司為了吸引網購者,特別推出“玩網絡游戲,送免費購物券”活動,網購者可根據拋擲骰子的結果,操控微型遙控車在方格圖上行進. 若遙控車最終停在“勝利大本營”,則網購者可獲得免費購物券500元;若遙控車最終停在“失敗大本營”,則網購者可獲得免費購物券200元. 已知骰子出現奇數與偶數的概率都是![]() ,方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,網購者每拋擲一次骰子,遙控車向前移動一次.若擲出奇數,遙控車向前移動一格(從
,方格圖上標有第0格、第1格、第2格、…、第20格。遙控車開始在第0格,網購者每拋擲一次骰子,遙控車向前移動一次.若擲出奇數,遙控車向前移動一格(從![]() 到
到![]() )若擲出偶數遙控車向前移動兩格(從
)若擲出偶數遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第
),直到遙控車移到第19格勝利大本營)或第20格(失敗大本營)時,游戲結束。設遙控車移到第![]() 格的概率為
格的概率為![]() ,試證明
,試證明![]() 是等比數列,并求網購者參與游戲一次獲得免費購物券金額的期望值.
是等比數列,并求網購者參與游戲一次獲得免費購物券金額的期望值.
附:在線性回歸方程![]() 中,
中,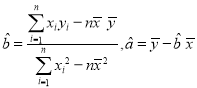 .
.
【答案】(1)![]() ,預計到2022年該公司的網購人數能超過300萬人;
,預計到2022年該公司的網購人數能超過300萬人;
(2)約400元.
【解析】
(1)依題意,先求出![]() ,代入公式即可得到
,代入公式即可得到![]() ,
,![]() ,可得回歸方程為
,可得回歸方程為![]() ,令
,令![]() ,
,![]() .所以預計到2022年該公司的網購人數能超過300萬;
.所以預計到2022年該公司的網購人數能超過300萬;
(2)遙控車移到第![]() (
(![]() )格的情況是下列兩種,而且也只有兩種.
)格的情況是下列兩種,而且也只有兩種.
①遙控車先到第![]() 格,又擲出偶數,其概率為
格,又擲出偶數,其概率為![]()
②遙控車先到第![]() 格,又擲出奇數,其概率為
格,又擲出奇數,其概率為![]()
所以![]() ,即可證得
,即可證得![]() 是等比數列,
是等比數列,
利用累加法求出數列![]() 的通項公式,即可求得失敗和獲勝的概率,從而計算出期望.
的通項公式,即可求得失敗和獲勝的概率,從而計算出期望.
解:(1)![]()
![]()
![]()
![]()
故![]() 從而
從而![]()
所以所求線性回歸方程為![]() ,
,
令![]() ,解得
,解得![]() .
.
故預計到2022年該公司的網購人數能超過300萬人
(2)遙控車開始在第0格為必然事件,![]() ,第一次擲骰子出現奇數,遙控車移到第一格,其概率為
,第一次擲骰子出現奇數,遙控車移到第一格,其概率為![]() ,即
,即![]() .遙控車移到第
.遙控車移到第![]() (
(![]() )格的情況是下列兩種,而且也只有兩種.
)格的情況是下列兩種,而且也只有兩種.
①遙控車先到第![]() 格,又擲出奇數,其概率為
格,又擲出奇數,其概率為![]()
②遙控車先到第![]() 格,又擲出偶數,其概率為
格,又擲出偶數,其概率為![]()
所以![]() ,
,![]()
![]() 當
當![]() 時,數列
時,數列![]() 是公比為
是公比為![]() 的等比數列
的等比數列
![]()
以上各式相加,得![]()
![]()
![]() (
(![]() ),
),
![]() 獲勝的概率
獲勝的概率![]()
失敗的概率![]()
![]() 設參與游戲一次的顧客獲得優惠券金額為
設參與游戲一次的顧客獲得優惠券金額為![]() 元,
元,![]() 或
或![]()
![]() X的期望
X的期望![]()
![]() 參與游戲一次的顧客獲得優惠券金額的期望值為
參與游戲一次的顧客獲得優惠券金額的期望值為![]() ,約400元.
,約400元.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f (x)= 的圖象在點(-2,f (-2))處的切線方程為16x+y+20=0.
的圖象在點(-2,f (-2))處的切線方程為16x+y+20=0.
(1)求實數a、b的值;
(2)求函數f(x)在區間[-1,2]上的最大值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代著名的![]() 周髀算經
周髀算經![]() 中提到:凡八節二十四氣,氣損益九寸九分六分分之一;冬至晷
中提到:凡八節二十四氣,氣損益九寸九分六分分之一;冬至晷![]() 長一丈三尺五寸,夏至晷長一尺六寸
長一丈三尺五寸,夏至晷長一尺六寸![]() 意思是:一年有二十四個節氣,每相鄰兩個節氣之間的日影長度差為
意思是:一年有二十四個節氣,每相鄰兩個節氣之間的日影長度差為![]() 分;且“冬至”時日影長度最大,為1350分;“夏至”時日影長度最小,為160分
分;且“冬至”時日影長度最大,為1350分;“夏至”時日影長度最小,為160分![]() 則“立春”時日影長度為
則“立春”時日影長度為![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過原點
,過原點![]() 且斜率為1的直線交橢圓
且斜率為1的直線交橢圓![]() 于
于![]() 兩點,四邊形
兩點,四邊形![]() 的周長與面積分別為12與
的周長與面積分別為12與![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與圓
與圓![]() 相切,且與橢圓
相切,且與橢圓![]() 交于
交于![]() 兩點,求原點到
兩點,求原點到![]() 的中垂線的最大距離.
的中垂線的最大距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的奇數項是首項為1的等差數列,偶數項是首項為2的等比數列.數列
的奇數項是首項為1的等差數列,偶數項是首項為2的等比數列.數列![]() 前
前![]() 項和為
項和為![]() ,且滿足
,且滿足![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 前
前![]() 項和
項和![]() ;
;
(3)在數列![]() 中,是否存在連續的三項
中,是否存在連續的三項![]() ,按原來的順序成等差數列?若存在,求出所有滿足條件的正整數
,按原來的順序成等差數列?若存在,求出所有滿足條件的正整數![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
如圖是某市12月1日-20日AQI指數變化趨勢:

下列敘述正確的是( )
A.這20天中AQI指數值的中位數略高于100
B.這20天中的中度污染及以上的天數占![]()
C.該市12月的前半個月的空氣質量越來越好
D.總體來說,該市12月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com