
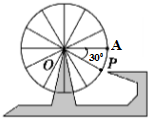
 如圖所示,一個半徑為10m的摩天輪,輪子的底部在地面上2m處,如果此摩天輪按逆時針方向轉動,每30s轉一圈,且當摩天輪上某人經過點P處(∠POA=30°)時開始計時.
如圖所示,一個半徑為10m的摩天輪,輪子的底部在地面上2m處,如果此摩天輪按逆時針方向轉動,每30s轉一圈,且當摩天輪上某人經過點P處(∠POA=30°)時開始計時.分析 (1)根據題意,求出t時摩天輪上某人所轉過的角度,計算此人相對于地面的高度h;
(2)根據高度h(m)的解析式,求出此人相對于地面的高度不小于17的時間.
解答 解:(1)根據題意,在t時,摩天輪上某人所轉過的角為$\frac{2π}{30}$t=$\frac{π}{15}$t,
故在t時,此人相對于地面的高度為
$h=10sin({\frac{π}{15}t-\frac{π}{6}})+12$(t≥0);…(6分)
(2)由$10sin({\frac{π}{15}t-\frac{π}{6}})+12$≥17,
得$sin({\frac{π}{15}t-\frac{π}{6}})$≥$\frac{1}{2}$,
則5≤t≤15;
故此人有10 s相對于地面的高度不小于17 m.…(12分)
點評 本題考查了三角函數模型的應用問題,是基礎題目.


科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
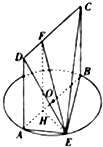 如圖,AB為圓O的直徑,E是圓O上不同于A,B的動點,四邊形ABCD為矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.
如圖,AB為圓O的直徑,E是圓O上不同于A,B的動點,四邊形ABCD為矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,3) | B. | $(3,\frac{16}{3})$ | C. | $(0,3)∪(3,\frac{16}{3})$ | D. | (0,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com