【題目】如圖，在四棱錐
中，四邊形
是邊長為8的菱形，
，
是等邊三角形，二面角
的余弦值為
.
（Ⅰ）求證：
；
（Ⅱ）求直線
與平面
夾角的正弦值.
字詞句段篇系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線C：
=2px經過點
（1，2）．過點Q（0，1）的直線l與拋物線C有兩個不同的交點A，B，且直線PA交y軸于M，直線PB交y軸于N．
（Ⅰ）求直線l的斜率的取值范圍；
（Ⅱ）設O為原點，
，
，求證：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
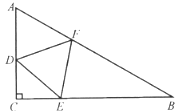
【題目】某小區打算將如圖的一直三角形
區域進行改建,在三邊上各選一點連成等邊三角形
,在其內建造文化景觀.已知
,
,則
區域內面積(單位：
)的最小值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為研究男、女生的身高差異，現隨機從高二某班選出男生、女生各10人，并測量他們的身高，測量結果如下（單位：厘米）：
男：164 178 174 185 170 158 163 165 161 170
女：165 168 156 170 163 162 158 153 169 172
（1）根據測量結果完成身高的莖葉圖（單位：厘米），并分別求出男、女生身高的平均值.
（2）請根據測量結果得到20名學生身高的中位數
（單位：厘米），將男、女生身高不低于和低于的人數填入下表中，并判斷是否有
的把握認為男、女生身高有差異？
人數 | 男生 | 女生 |
身高 | ||
身高 |
參照公式：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
（3）若男生身高低于165厘米為偏矮，不低于165厘米且低于175厘米為正常，不低于175厘米為偏高.假設可以用測量結果的頻率代替概率，試求從高二的男生中任意選出2人，恰有1人身高屬于正常的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知F1，F2分別是橢圓C：
1（＞b＞0）的左、右焦點，過F2且不與x軸垂直的動直線l與橢圓交于M，N兩點，點P是橢圓C右準線上一點，連結PM，PN，當點P為右準線與x軸交點時有2PF2＝F1F2．
（1）求橢圓C的離心率；
（2）當點P的坐標為（2，1）時，求直線PM與直線PN的斜率之和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題
①已知
為橢圓
上任意一點，
，
是橢圓的兩個焦點，則
的周長是8；
②已知
是雙曲線
上任意一點，
是雙曲線的右焦點，則
；
③已知直線
過拋物線
的焦點，且與
交于
，
，
，
兩點，則
；
④橢圓具有這樣的光學性質：從橢圓的一個焦點出發的光線，經橢圓反射后，反射光線經過橢圓的另一個焦點，今有一個水平放置的橢圓形臺球盤，點，是它的焦點，長軸長為
，焦距為
，若靜放在點的小球（小球的半徑忽略不計）從點沿直線出發則經橢圓壁反射后第一次回到點時，小球經過的路程恰好是
．
其中正確命題的序號為__（請將所有正確命題的序號都填上）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面上的線段
及點
，任取上一點
，線段
長度的最小值稱為點到線段的距離，記作
.請你寫出到兩條線段
，
距離相等的點的集合
，
，
，其中
，
，
，
，
，
是下列兩組點中的一組．對于下列兩種情形，只需選做一種，滿分分別是① 3分；② 5分．① 
，
，
，
；② ，，，
．你選擇第_____種情形，到兩條線段，距離相等的點的集合
_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
