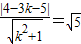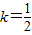某圓經過點A(2,-3)和B(-2,-5)
①若圓的面積最小,求圓的方程.
②過C(3,-5)向①中圓作切線,求切線的方程.
【答案】
分析:①要使圓的面積最小,線段AB為圓的直徑,線段AB的中點坐標即為所求圓的圓心,利用兩點間的距離公式求出線段AB長度的一半即為圓的半徑,根據求出的圓心和半徑寫出圓的標準方程即可.
②先假設切線方程,再利用圓心到直線的距離等于半徑,建立方程,即可求切線的方程.
解答:解:①要使圓的面積最小,則AB為圓的直徑,
∵點A(2,-3)和B(-2,-5)
∴AB的中點坐標為(0,-4)
即所求圓心坐標為(0,-4),
而|AB|=
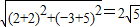
,所以圓的半徑r=
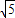
,
∴所求圓的方程為:x
2+(y+4)
2=5.
②設切線方程為:y+5=k(x-3),即kx-y-3k-5=0
利用圓心到直線的距離等于半徑可得:
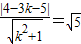
∴2k
2+3k-2=0
∴k=-2或
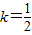
∴切線方程為:2x+y-1=0或x-2y-13=0
點評:本題重點考查圓的方程,考查圓的切線方程,靈活運用中點坐標公式及兩點間的距離公式化簡求值,是解題的關鍵.

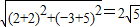 ,所以圓的半徑r=
,所以圓的半徑r=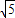 ,
,