
【題目】已知一個正四面體和一個正四棱錐,它們的各條棱長均相等,則下列說法:
①它們的高相等;②它們的內切球半徑相等;③它們的側棱與底面所成的線面角的大小相等;④若正四面體的體積為![]() ,正四棱錐的體積為
,正四棱錐的體積為![]() ,則
,則![]() ;⑤它們能拼成一個斜三棱柱.其中正確的個數為( )
;⑤它們能拼成一個斜三棱柱.其中正確的個數為( )
A.1個B.2個C.3個D.4個
【答案】B
【解析】
①,正四面體的高![]() ,正四棱錐的高
,正四棱錐的高![]() ,所以該命題錯誤;
,所以該命題錯誤;
②,設正四面體的內切球半徑為![]()
![]() .設正四棱錐的內切球半徑為
.設正四棱錐的內切球半徑為![]() 則
則![]() .所以該命題不正確;
.所以該命題不正確;
③,在正四面體中,![]() 就是側棱和底面所成的角,
就是側棱和底面所成的角,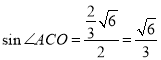 .在正四棱錐中,
.在正四棱錐中,![]() 就是側棱和底面所成的角,
就是側棱和底面所成的角,![]() ,所以該命題不正確;
,所以該命題不正確;
④,計算得![]() .所以該命題正確;
.所以該命題正確;
⑤,把一個斜三棱柱分解成一個正四面體和正四棱錐,所以該命題正確.
設正四面體和正四棱錐的棱長都為![]() ,
,
①,![]() ,
,
所以正四面體的高![]() .
.
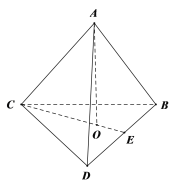
如圖,正四棱錐的棱長都為2,它的高![]() ,
,
所以該命題不正確;
②,設正四面體的內切球半徑為![]()
則![]() ,所以
,所以![]() .
.
設正四棱錐的內切球半徑為![]() 則
則
![]() ,所以
,所以![]() .
.
所以該命題不正確;
③,在正四面體中,![]() 就是側棱和底面所成的角,
就是側棱和底面所成的角,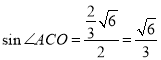 .
.
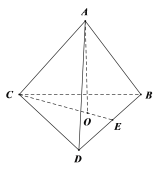
在正四棱錐中,![]() 就是側棱和底面所成的角,
就是側棱和底面所成的角,![]() ,
,
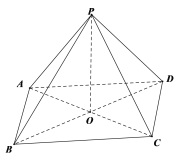
所以該命題不正確;
④,若正四面體的體積為![]() ,
,![]() ,
,
正四棱錐的體積為![]() ,
,![]() ,則
,則![]() .
.
所以該命題正確;
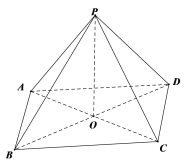
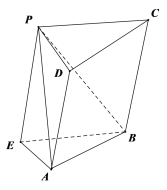
⑤,如圖,是一個斜三棱柱,其中四棱錐![]() 是一個棱長都為2的正四棱錐,四面體
是一個棱長都為2的正四棱錐,四面體![]() 是棱長都為2的正四面體,所以它們能拼成一個斜三棱柱.所以該命題正確.
是棱長都為2的正四面體,所以它們能拼成一個斜三棱柱.所以該命題正確.
故選:B.


科目:高中數學 來源: 題型:
【題目】某學校近幾年來通過“書香校園”主題系列活動,倡導學生整本閱讀紙質課外書籍.下面的統計圖是該校2013年至2018年紙質書人均閱讀量的情況,根據統計圖提供的信息,下列推斷不合理的是( )
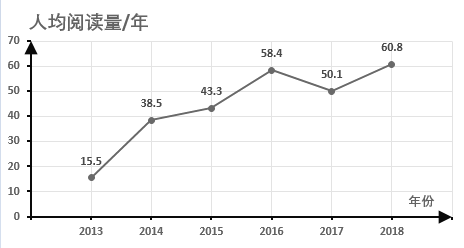
A.從2013年到2016年,該校紙質書人均閱讀量逐年增長
B.2013年至2018年,該校紙質書人均閱讀量的中位數是46.7本
C.2013年至2018年,該校紙質書人均閱讀量的極差是45.3本
D.2013年至2018年,該校后三年紙質書人均閱讀量總和是前三年紙質書人均閱讀量總和的2倍
查看答案和解析>>
科目:高中數學 來源: 題型:
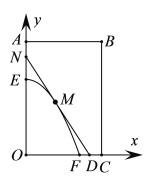
【題目】如圖,某小區有一塊矩形地塊![]() ,其中
,其中![]() ,
,![]() ,單位:百米.已知
,單位:百米.已知![]() 是一個游泳池,計劃在地塊
是一個游泳池,計劃在地塊![]() 內修一條與池邊
內修一條與池邊![]() 相切于點
相切于點![]() 的直路
的直路![]() (寬度不計),交線段
(寬度不計),交線段![]() 于點
于點![]() ,交線段
,交線段![]() 于點
于點![]() .現以點
.現以點![]() 為坐標原點,以線段
為坐標原點,以線段![]() 所在直線為
所在直線為![]() 軸,建立平面直角坐標系,若池邊
軸,建立平面直角坐標系,若池邊![]() 滿足函數
滿足函數![]() 的圖象,若點
的圖象,若點![]() 到
到![]() 軸距離記為
軸距離記為![]() .
.
(1)當![]() 時,求直路所在的直線方程;
時,求直路所在的直線方程;
(2)當![]() 為何值時,地塊
為何值時,地塊![]() 在直路
在直路![]() 不含泳池那側的面積取到最大,最大值時多少?
不含泳池那側的面積取到最大,最大值時多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩種樹苗中各抽測了10株樹苗的高度,其莖葉圖數據如圖.根據莖葉圖,下列描述正確的是( )
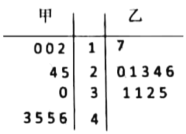
A.甲種樹苗的中位數大于乙種樹苗的中位數,且甲種樹苗比乙種樹苗長得整齊
B.甲種樹苗的中位數大于乙種樹苗的中位數,但乙種樹苗比甲種樹苗長得整齊
C.乙種樹苗的中位數大于甲種樹苗的中位數,且乙種樹苗比甲種樹苗長得整齊
D.乙種樹苗的中位數大于甲種樹苗的中位數,但甲種樹苗比乙種樹苗長得整齊
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)求![]() 在點P(1,
在點P(1,![]() )處的切線方程;
)處的切線方程;
(2)若關于x的不等式![]() 有且僅有三個整數解,求實數t的取值范圍;
有且僅有三個整數解,求實數t的取值范圍;
(3)若![]() 存在兩個正實數
存在兩個正實數![]() ,
,![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,
為等差數列,![]() ,
,![]() ,
,![]() 分別是下表第一、二、三行中的某一個數,且
分別是下表第一、二、三行中的某一個數,且![]() ,
,![]() ,
,![]() 中的任何兩個數都不在下表的同一列.
中的任何兩個數都不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | |||
第二行 | 4 | 6 | 9 |
第三行 | 12 | 8 | 7 |
請從①![]() ,②
,②![]() ,③
,③ ![]() 的三個條件中選一個填入上表,使滿足以上條件的數列
的三個條件中選一個填入上表,使滿足以上條件的數列![]() 存在;并在此存在的數列
存在;并在此存在的數列![]() 中,試解答下列兩個問題
中,試解答下列兩個問題
(1)求數列![]() 的通項公式;
的通項公式;
(2)設數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com