
分析 由約束條件作出可行域,化目標函數為直線方程的斜截式,數形結合得到最優解,聯立方程組求得最優解的坐標,代入目標函數得答案.
解答 解:由約束條件$\left\{\begin{array}{l}{2x+y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$作出可行域如圖,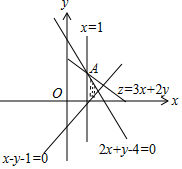
聯立$\left\{\begin{array}{l}{x=1}\\{2x+y-4=0}\end{array}\right.$,解得A(1,2),
化目標函數z=3x+2y為y=$-\frac{3}{2}x+\frac{z}{2}$,由圖可知,當直線y=$-\frac{3}{2}x+\frac{z}{2}$過A時,直線在y軸上的截距最大,z有最大值為7.
故答案為:7.
點評 本題考查簡單的線性規劃,考查了數形結合的解題思想方法,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
| A組 | B組 | 合計 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合計 | 56 | 44 | 100 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
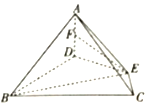 如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“?x0∈R,x02-x0≤0”的否定為“?x∈R,x2-x>0” | |
| B. | 命題“在△ABC中,A>30°,則sinA>$\frac{1}{2}$”的逆否命題為真命題 | |
| C. | 設{an}是公比為q的等比數列,則“q>1”是“{an}為遞增數列”的充分必要條件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$滿足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,則$\overrightarrow a$與$\overrightarrow b$共線 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -2017 | C. | 2017 | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com