
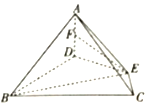
 如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如圖,在四棱錐A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.分析 (1)取DB中點G,連結EG、FG.證面EGF∥平面ABC,即可得EF∥平面ABC.
(2)以點D為原點,建立如圖所示的直角坐標系D-xyz,則A(0,0,$\sqrt{3}$),E(0,$\sqrt{3}$,0),B(2,0,0),C($\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$,0).求出平面ACE的法向量即可
解答 證明:(1)取DB中點G,連結EG、FG.
∵F是AD的中點,∴FG∥AB.
∵BD=2CE,∴BG=CE.
∵∠DBC=∠BCE
∴E、G到直線BC的距離相等,則BG∥CB,
∵EG∩FG=G
∴面EGF∥平面ABC,則EF∥平面ABC.
解:(2)以點D為原點,建立如圖所示的直角坐標系D-xyz,設EC=1,則DB=2,取BC中點C,則EG∥BC,∴BC=3,
∵AD=DE,則A(0,0,$\sqrt{3}$),E(0,$\sqrt{3}$,0),B(2,0,0),C($\frac{1}{2}$,$\frac{3\sqrt{3}}{2}$,0).
$\overrightarrow{AE}=(0,\sqrt{3,}-\sqrt{3}),\overrightarrow{EC}=(\frac{1}{2},\frac{\sqrt{3}}{2},0)$,$\overrightarrow{EB}=(2,-\sqrt{3},0)$.
設平面ACE的法向量$\overrightarrow{n}=(x,y,z)$,
$\overrightarrow{n}•\overrightarrow{AE}=\sqrt{3}x-\sqrt{3}y=0,\overrightarrow{n}•\overrightarrow{EC}$=$\frac{1}{2}$x+$\frac{\sqrt{3}}{2}$y=0
令y=1,則$;\\;\\;\\;\overrightarrow{n}=(-\sqrt{3},1,1)$$\overrightarrow{n}=(-\sqrt{3},1,1)$,|cos$<\overrightarrow{n},\overrightarrow{EB}>$|=$\frac{3\sqrt{3}}{\sqrt{5}×\sqrt{7}}=\frac{3\sqrt{105}}{35}$.
∴BE與平面ACE所成角的正弦值為:$\frac{3\sqrt{105}}{35}$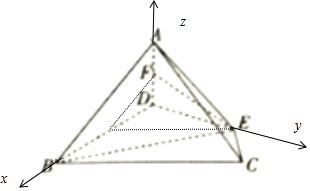
點評 本題考查了線面平行,向量法求線面角,屬于中檔題.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-$\frac{1}{e}$) | B. | (-∞,-e) | C. | (e,+∞) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 1 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com