
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
分析 要求三點共線問題,先求每兩點對應的向量,然后再按兩向量共線進行判斷,本題知道$\overrightarrow{AB}$,要根據$\overrightarrow{BC}$和$\overrightarrow{CD}$算出$\overrightarrow{BD}$,再用向量共線的充要條件.
解答 解:因為$\overrightarrow{AB}$=2$\overrightarrow{a}+p\overrightarrow{b}$,$\overrightarrow{BC}=\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{CD}=(q-1)\overrightarrow{a}-2\overrightarrow{b}$,
$\overrightarrow{BD}$=(2+q)$\overrightarrow{a}$+(p-1)$\overrightarrow{b}$,
又A,B,D三點共線,
∴$\overrightarrow{AB}=λ\overrightarrow{BD}$,
∴λ(2+q)=2,λ(p-1)=p,
化簡得pq=-2,
故選D.
點評 本題考查三點共線問題,注意使用三點共線的充要條件,三點共線實質上就是兩向量共線,容易出錯的是向量共線的坐標形式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
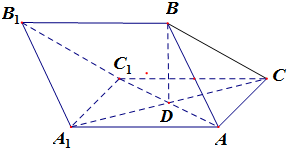 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1與A1C相交于點D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1與A1C相交于點D.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
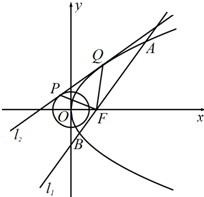 如圖,設拋物線C:y2=2px(p>0)的焦點為F,過點F的直線l1交拋物線C于A,B兩點,且|AB|=8,線段AB的中點到y軸的距離為3.直線l2與圓${x^2}+{y^2}=\frac{1}{2}$切于點P,與拋物線C切于點Q,則△FPQ的面積( )
如圖,設拋物線C:y2=2px(p>0)的焦點為F,過點F的直線l1交拋物線C于A,B兩點,且|AB|=8,線段AB的中點到y軸的距離為3.直線l2與圓${x^2}+{y^2}=\frac{1}{2}$切于點P,與拋物線C切于點Q,則△FPQ的面積( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{{\sqrt{3}}}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
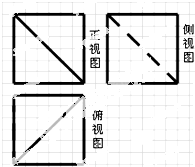 如圖,網格紙上小正方形的邊長為1,粗線畫出的是一正方體被截去一部分后所得幾何體的三視圖,則該幾何體的表面積為( )
如圖,網格紙上小正方形的邊長為1,粗線畫出的是一正方體被截去一部分后所得幾何體的三視圖,則該幾何體的表面積為( )| A. | 54 | B. | 162 | C. | 54+18$\sqrt{3}$ | D. | 162+18$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com