
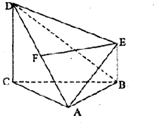
 如圖,四棱錐A-BCDE中,F為AD的中點,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.
如圖,四棱錐A-BCDE中,F為AD的中點,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.分析 (1)取AC中點O,連結BO、FO,推導出EF⊥OF,EF⊥AC,由此能證明EF⊥平面ACD.
(2)以O為原點,OA為x軸,OB為y軸,OF為z軸,建立空間直角坐標系,利用向量法能求出平面ADE與平面ABD所成銳二面角的余弦值.
解答 證明:(1)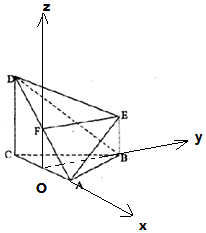 取AC中點O,連結BO、FO,
取AC中點O,連結BO、FO,
∵四棱錐A-BCDE中,F為AD的中點,DC⊥平面ABC,
CD∥BE,AB=AC=BC=CD=2BE,
∴OF$\underset{∥}{=}$BE,BE⊥OB,∴四邊形CBEF是矩形,
∴EF⊥OF,EF⊥AC,
∵OF∩AC=O,∴EF⊥平面ACD.
解:(2)以O為原點,OA為x軸,OB為y軸,OF為z軸,建立空間直角坐標系,
設AB=AC=BC=CD=2BE=2,
則A(1,0,0),B(0,$\sqrt{3}$,0),D(-1,0,2),E(0,$\sqrt{3}$,1),
$\overrightarrow{AB}$=(-1,$\sqrt{3}$,0),$\overrightarrow{AD}$=(-2,0,2),$\overrightarrow{AE}$=(-1,$\sqrt{3},1$),
設平面ADE的法向量$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{AD}•\overrightarrow{n}=-2x+2z=0}\\{\overrightarrow{AE}•\overrightarrow{n}=-x+\sqrt{3}y+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
設平面ABD的法向量$\overrightarrow{m}$=(a,b,c),
則$\left\{\begin{array}{l}{\overrightarrow{AB}•\overrightarrow{m}=-a+\sqrt{3}b=0}\\{\overrightarrow{AD}•\overrightarrow{m}=-2a+2c=0}\end{array}\right.$,取a=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3},1,\sqrt{3}$),
設平面ADE與平面ABD所成銳二面角為θ,
則cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2\sqrt{3}}{\sqrt{2}•\sqrt{5}}$=$\frac{\sqrt{30}}{5}$.
∴平面ADE與平面ABD所成銳二面角的余弦值為$\frac{\sqrt{30}}{5}$.
點評 本題考查線面垂直的證明,考查二面角的余弦值的求法,是中檔題,解題時要認真審題,注意向量法的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n=1驗證不正確 | B. | 歸納假設不正確 | ||
| C. | 從n=k到n=k+1的推理不正確 | D. | 證明過程完全正確 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
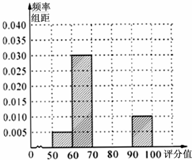 某單位進行了主題為“你幸福嗎”的幸福指數問卷調查,得到每個調查對象的幸福指數評分值(百分制).現從收到的調查表中隨機抽取20份進行統計,得到如圖所示的頻率分布表和頻率分布直方圖.
某單位進行了主題為“你幸福嗎”的幸福指數問卷調查,得到每個調查對象的幸福指數評分值(百分制).現從收到的調查表中隨機抽取20份進行統計,得到如圖所示的頻率分布表和頻率分布直方圖.| 幸福指數評分值 | 頻數 | 頻率 |
| [50,60] | ||
| (60,70] | ||
| (70,80] | ||
| (80,90] | 3 | |
| (90,100] | ||
| 合 計 | 20 | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{7π}{12}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{5π}{12}$ | D. | $x=\frac{π}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com