
分析 (I)a1=2,an+1=2(Sn+n+1)(n∈N*),可得a2=8.利用遞推關系可得:an+1=3an+2,變形為:an+1+1=3(an+1),即bn+1=3bn,即可證明.
(II)由(I)可得:bn=3n.利用“錯位相減法”與等比數列的求和公式即可得出.
(III)bn=3n=an+1,解得an=3n-1.由$\frac{1}{{a}_{k}}$=$\frac{1}{{3}^{k}-1}>$$\frac{1}{{3}^{k}}$,即可證明左邊不等式成立.又由$\frac{1}{{a}_{k}}$=$\frac{1}{{3}^{k}-1}$=$\frac{{3}^{k+1}-1}{({3}^{k}-1)({3}^{k+1}-1)}$<$\frac{{3}^{k+1}}{({3}^{k}-1)({3}^{k+1}-1)}$=$\frac{3}{2}(\frac{1}{{3}^{k}-1}-\frac{1}{{3}^{k+1}-1})$,即可證明右邊不等式成立.
解答 (I)證明:a1=2,an+1=2(Sn+n+1)(n∈N*),∴a2=2×(2+1+1)=8.
n≥2時,an=2(Sn-1+n),相減可得:an+1=3an+2,變形為:an+1+1=3(an+1),n=1時也成立.
令bn=an+1,則bn+1=3bn.∴{bn}是等比數列,首項為3,公比為3.
(II)解:由(I)可得:bn=3n.
∴數列{nbn}的前n項和Tn=3+2×32+3×33+…+n•3n,
3Tn=32+2×33+…+(n-1)•3n+n•3n+1,
∴-2Tn=3+32+…+3n-n•3n+1=$\frac{3({3}^{n}-1)}{3-1}$-n•3n+1=$\frac{1-2n}{2}$×3n+1-$\frac{3}{2}$,
解得Tn=$\frac{2n-1}{4}×{3}^{n+1}$+$\frac{3}{4}$.
(III)證明:∵bn=3n=an+1,解得an=3n-1.
由$\frac{1}{{a}_{k}}$=$\frac{1}{{3}^{k}-1}>$$\frac{1}{{3}^{k}}$.
∴$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$>$\frac{1}{3}+\frac{1}{{3}^{2}}+$…+$\frac{1}{{3}^{n}}$=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=$\frac{1}{2}-\frac{1}{2}×\frac{1}{{3}^{n}}$,因此左邊不等式成立.
又由$\frac{1}{{a}_{k}}$=$\frac{1}{{3}^{k}-1}$=$\frac{{3}^{k+1}-1}{({3}^{k}-1)({3}^{k+1}-1)}$<$\frac{{3}^{k+1}}{({3}^{k}-1)({3}^{k+1}-1)}$=$\frac{3}{2}(\frac{1}{{3}^{k}-1}-\frac{1}{{3}^{k+1}-1})$,
可得$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$\frac{1}{2}$+$\frac{3}{2}[(\frac{1}{{3}^{2}-1}-\frac{1}{{3}^{3}-1})$+$(\frac{1}{{3}^{3}-1}-\frac{1}{{3}^{4}-1})$…+$(\frac{1}{{3}^{n}-1}-\frac{1}{{3}^{n+1}-1})]$
=$\frac{1}{2}+\frac{3}{2}(\frac{1}{8}-\frac{1}{{3}^{n+1}-1})$<$\frac{11}{16}$.因此右邊不等式成立.
綜上可得:$\frac{1}{2}$-$\frac{1}{2×{3}^{n}}$<$\frac{1}{{a}_{1}}$$+\frac{1}{{a}_{2}}$$+\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$$<\frac{11}{16}$.
點評 本題考查了等比數列的通項公式與求和公式、數列遞推關系、“錯位相減法”、“放縮法”、不等式的性質,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:解答題
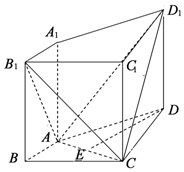 如圖,在四棱柱ABCD-A1B1C1D1中,側棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.
如圖,在四棱柱ABCD-A1B1C1D1中,側棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-2≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1≤x≤2} | D. | {x|-3≤x≤2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖,已知矩形ABCD,AD=2,E為AB邊上的點,現將△ADE沿DE翻折至△A′DE,使得點A′在平面EBCD上的投影在CD上,且直線A′D與平面EBCD所成角為45°,則線段AE的長為2$\sqrt{2}$.
如圖,已知矩形ABCD,AD=2,E為AB邊上的點,現將△ADE沿DE翻折至△A′DE,使得點A′在平面EBCD上的投影在CD上,且直線A′D與平面EBCD所成角為45°,則線段AE的長為2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 已知扇環如圖所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇環邊界上一動點,且滿足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,則2x+y的取值范圍為[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].
已知扇環如圖所示,∠AOB=120°,OA=2,OA′=$\frac{1}{2}$,P是扇環邊界上一動點,且滿足$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,則2x+y的取值范圍為[$\frac{1}{4}$,$\frac{2\sqrt{21}}{3}$].查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com