Question

（08年北師大附中月考文） 已知四棱錐P―ABCD的底面為直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA = AD = DC =AB = 1.

（I）證明：面PAD⊥面PCD；

（II）求AC與PB所成角的余弦值；

（III）求面PAB與面PBC所成的二面角的大小

 

Answer 1

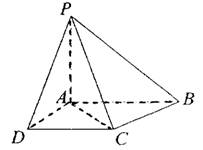
解析：（I）證明：∵PA⊥底面ABCD，CD⊥AD，

∴由三垂線定理，得CD⊥PD，

∵CD⊥AD，CD⊥PD，且PD∩AD=D，

∴CD⊥平面PAD，

∵CD平面PCD，

∴面PAD⊥面PCD。

   （II）解：過點B作BE//CA，且BE=CA，連結AE。

    則∠PBE是AC與PB所成的角，

    可求得AC = CB = BE = EA =。

    又AB=2，所以四邊形ACBE為正方形，∴BE⊥AE，

∵PA⊥底面ABCD。 ∴PA⊥BE，

∴BE⊥面PAE。

∴BE⊥PE，即∠PEB=90°

在Rt△PAB中，得PB=。

在Rt△PEB中，

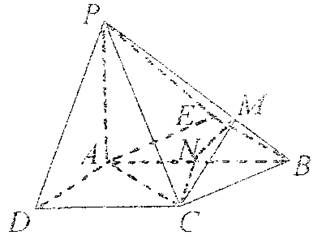
   （III）解：過點C作CN⊥AB于N，過點N作NM⊥PB于M，連結CM，

則MN是CM在面PAB上的射影。由三垂線定理，得CM⊥PB。

∴∠CMN為面PAB與面PBC所成的二面角的平面角。

可求得CN = 1，CM=