Question

正態總體N（0，1）的概率密度函數是f(x)=,x∈R.

（1）求證：ｆ（ｘ）是偶函數；

（2）求ｆ（ｘ）的最大值；

（3）利用指數函數的性質說明ｆ（ｘ）的增減性.

Answer 1

思路分析： 對給出的標準正態分布的概率密度函數，可以利用函數的相關知識來研究它的相關性質.

解：（1）對于任意的x∈R,f(-x)===f(x).

所以ｆ（ｘ）是偶函數；

（2）令z=,當ｘ=0時，z=0,e^x=1,

∵e^x是關于ｚ的增函數，當ｘ≠0時，z＞0,e^x＞1，

∴當ｘ=0，即ｚ=0時，=e^x取得最小值，當ｘ=0時，f(x)=取得最大值

（3）任取x₁＜0,x₂＜0,且x₁＜x₂,有x₁²＞x₂²,

∴

所以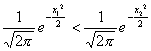,即f(x₁)＜f(x₂).

    這表明當ｘ＜0時，ｆ（ｘ）是遞增的.同理可得，對于任取的x₁＞0,x₂＞0,且x₁＜x₂，有f（x₁）＞f(x₂)，即當ｘ＞0時，ｆ（ｘ）是遞減的.