
【題目】(1)設![]() 是給定實數,解關于
是給定實數,解關于![]() 的不等式
的不等式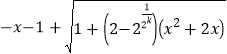
![]() ;
;
(2)設![]() 是一個給定實數,試求出1中
是一個給定實數,試求出1中![]() 的取值范圍,使得不等式
的取值范圍,使得不等式![]() 能滿足1中的式子。
能滿足1中的式子。
【答案】(1)見解析;(2)見解析
【解析】
(1)原不等式


下面對![]() 的取值分三種情形討論:
的取值分三種情形討論:
ⅰ.若![]() ,則式①變為
,則式①變為![]() ,即
,即![]() .
.
ⅱ.若![]() ,則
,則![]() ,顯然
,顯然![]() 滿足式①.
滿足式①.
下設![]() ,則式①
,則式①





![]()
 .
.
故當![]() 時,原不等式的解為
時,原不等式的解為 .
.
綜合ⅰ、ⅱ知,當![]() 時,原不等式的解為
時,原不等式的解為 .
.
ⅲ.若![]() ,則
,則![]() .
.
式①左邊的定義域為



下面再考慮式①的右邊, 分成三種情形:
a.若![]() ,即
,即![]() ,亦即
,亦即![]() ,此時,顯然
,此時,顯然![]() 滿足式①.
滿足式①.
下設![]() ,則式①
,則式①
 。
。
(過程同ⅱ完全一樣)所以,當![]() 時,原不等式的解為
時,原不等式的解為

 ,
,
又當![]() 時,有
時,有

![]()
 ,顯然成立.
,顯然成立.
因此,當![]() 時,原不等式的解為
時,原不等式的解為
 。
。
b.若![]() ,即
,即![]() ,此時,式①的右邊為0,則由式②得,當
,此時,式①的右邊為0,則由式②得,當![]() 時,原不等式的解為
時,原不等式的解為
 ,
,
即![]()
c.若![]() ,即
,即![]() ,此時,
,此時,![]() 滿足式①(因為式①的右邊小于0)
滿足式①(因為式①的右邊小于0)
下設![]() ,即
,即![]() ,此時,式①的右邊大于或等于0,則式①
,此時,式①的右邊大于或等于0,則式①

 .
.
故當![]() 時,原不等式的解恰好是式②.
時,原不等式的解恰好是式②.
(2)由1的結論可知,當![]() 時,都不合題目要求,只須考慮
時,都不合題目要求,只須考慮![]() 。
。
當![]() 時,令
時,令![]() ,顯然
,顯然![]() 。
。
由1的結論得
![]() ,
,
即![]()
下面對![]() 分兩種情形討論。
分兩種情形討論。
ⅰ.當![]() ,即
,即![]() 時,式③顯然成立,故當
時,式③顯然成立,故當![]() 時,
時,![]() 符合題目要求。
符合題目要求。
ⅱ.當![]() ,即
,即![]() 時,式③
時,式③
![]()
a.若![]() ,即
,即![]() ,
,
則式④顯然成立,故當
![]() 時,
時,![]() 符合題目要求
符合題目要求
b.若![]() ,即
,即![]() ,則式④
,則式④![]()
![]()
![]()
![]()
![]() .
.
令![]() .
.
易知![]() 是
是![]() 的增函數,
的增函數,![]() 的解為
的解為![]() ,當
,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
【題目】根據以往的經驗,某工程施工期間的降水量![]() (單位:
(單位:![]() )對工期的影響如下表:
)對工期的影響如下表:
降水量 |
|
|
|
|
工期延誤天數 |
|
|
|
|
歷年氣象資料表明,該工程施工期間降水量![]() 小于
小于![]() 、
、![]() 、
、![]() 的概率分別為
的概率分別為![]() 、
、![]() 、
、![]() ,求:
,求:
(1)在降水量![]() 至少是
至少是![]() 的條件下,工期延誤不超過
的條件下,工期延誤不超過![]() 天的概率;
天的概率;
(2)工期延誤天數![]() 的均值與方差.
的均值與方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人民生活水平的提高,對城市空氣質量的關注度也逐步增大,圖2是某城市1月至8月的空氣質量檢測情況,圖中一、二、三、四級是空氣質量等級, 一級空氣質量最好,一級和二級都是質量合格天氣,下面四種說法正確的是( )
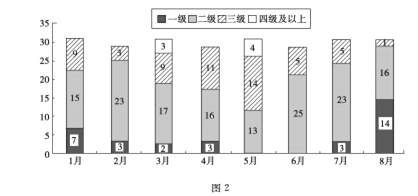
①1月至8月空氣合格天數超過20天的月份有5個
②第二季度與第一季度相比,空氣達標天數的比重下降了
③8月是空氣質量最好的一個月
④6月份的空氣質量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-ABCD中,平面![]() 垂直于對角線AC,且平面
垂直于對角線AC,且平面![]() 截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
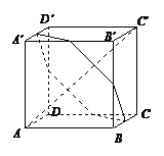
A. S為定值,l不為定值 B. S不為定值,l為定值
C. S與l均為定值 D. S與l均不為定值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com