
【題目】如圖,在正方體ABCD-ABCD中,平面![]() 垂直于對角線AC,且平面
垂直于對角線AC,且平面![]() 截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
截得正方體的六個表面得到截面六邊形,記此截面六邊形的面積為S,周長為l,則( )
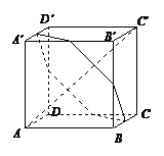
A. S為定值,l不為定值 B. S不為定值,l為定值
C. S與l均為定值 D. S與l均不為定值
【答案】B
【解析】
將正方體切去兩個正三棱錐![]() 和
和![]() ,得到一個幾何體
,得到一個幾何體![]() ,
,![]() 是以平行平面
是以平行平面![]() 和
和![]() 為上下底,每個側面都是直角等腰三角形,截面多邊形的每一條邊分別與
為上下底,每個側面都是直角等腰三角形,截面多邊形的每一條邊分別與![]() 的底面上的一條邊平行,設正方體棱長為
的底面上的一條邊平行,設正方體棱長為![]() ,
,![]() ,可求得六邊形的周長為
,可求得六邊形的周長為![]() 與
與![]() 無關,即周長為定值;當
無關,即周長為定值;當![]() 都在對應棱的中點時,
都在對應棱的中點時,![]() 是正六邊形,計算可得面積
是正六邊形,計算可得面積![]() ,當
,當![]() 無限趨近于
無限趨近于![]() 時,
時,![]() 的面積無限趨近于
的面積無限趨近于![]() ,從而可知
,從而可知![]() 的面積一定會發生變化。
的面積一定會發生變化。
設平面![]() 截得正方體的六個表面得到截面六邊形為
截得正方體的六個表面得到截面六邊形為![]() ,
,![]() 與正方體的棱的交點分別為
與正方體的棱的交點分別為![]() (如下圖),
(如下圖),
將正方體切去兩個正三棱錐![]() 和
和![]() ,得到一個幾何體
,得到一個幾何體![]() ,
,![]() 是以平行平面
是以平行平面![]() 和
和![]() 為上下底,每個側面都是直角等腰三角形,截面多邊形
為上下底,每個側面都是直角等腰三角形,截面多邊形![]() 的每一條邊分別與
的每一條邊分別與![]() 的底面上的一條邊平行,設正方體棱長為
的底面上的一條邊平行,設正方體棱長為![]() ,
,![]() ,則
,則![]() ,
,![]() ,故
,故![]() ,同理可證明
,同理可證明![]() ,故六邊形
,故六邊形![]() 的周長為
的周長為![]() ,即周長為定值;
,即周長為定值;
當![]() 都在對應棱的中點時,
都在對應棱的中點時,![]() 是正六邊形,計算可得面積
是正六邊形,計算可得面積![]() ,三角形
,三角形![]() 的面積為
的面積為![]() ,當
,當![]() 無限趨近于
無限趨近于![]() 時,
時,![]() 的面積無限趨近于
的面積無限趨近于![]() ,故
,故![]() 的面積一定會發生變化,不為定值。
的面積一定會發生變化,不為定值。
故答案為B.


科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與直線
與直線![]() 相切且與圓
相切且與圓![]() 外切。
外切。
(1)求圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設第一象限內的點![]() 在軌跡
在軌跡![]() 上,若
上,若![]() 軸上兩點
軸上兩點![]() ,
,![]() ,滿足
,滿足![]() 且
且![]() . 延長
. 延長![]() 、
、![]() 分別交軌跡
分別交軌跡![]() 于
于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 的斜率
的斜率![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為探索課堂教學改革,惠來縣某中學數學老師用傳統教學和“導學案”兩種教學方式,在甲、乙兩個平行班進行教學實驗.為了解教學效果,期末考試后,分別從兩個班級各隨機抽取20名學生的成績進行統計,得到如下莖葉圖.記成績不低于70分者為“成績優良”.
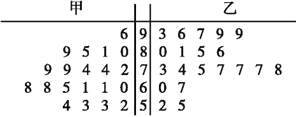
(Ⅰ)分析甲、乙兩班的樣本成績,大致判斷哪種教學方式的教學效果更佳,并說明理由;
(Ⅱ)由以上統計數據完成下面的![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“成績是否優良與教學方式有關”?
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為“成績是否優良與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優良 | |||
成績不優良 | |||
總計 |
參考公式:![]() ,其中
,其中![]() 是樣本容量.
是樣本容量.
獨立性檢驗臨界值表:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點A(-1,0),F(2,0),定直線l:x=![]() ,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
(Ⅰ)求E的方程;
(Ⅱ)試判斷以線段MN為直徑的圓是否過點F,并說明理由.![]()
![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調研高中生的作文水平.在某市普通高中的某次聯考中,參考的文科生與理科生人數之比為![]() ,且成績分布在
,且成績分布在![]() 的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中
的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中![]() 構成以2為公比的等比數列.
構成以2為公比的等比數列.
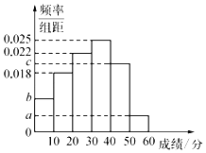
(1)求![]() 的值;
的值;
(2)填寫下面![]() 列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
文科生 | 理科生 | 合計 | |
獲獎 | 6 | ||
不獲獎 | |||
合計 | 400 |
(3)將上述調查所得的頻率視為概率,現從全市參考學生中,任意抽取2名學生,記“獲得優秀作文”的學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附: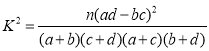 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com