
【題目】有下列命題中錯誤的是( )
A.![]() 是函數
是函數![]() 的極值點;
的極值點;
B.若![]() ,則
,則![]() ;
;
C.函數![]() 的最小值為2;
的最小值為2;
D.函數![]() 的定義域為[1,2],則函數
的定義域為[1,2],則函數![]() 的定義域為[2,4].
的定義域為[2,4].
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】洛薩![]() 科拉茨
科拉茨![]() Collatz,
Collatz,![]() 是德國數學家,他在1937年提出了一個著名的猜想:任給一個正整數n,如果n是偶數,就將它減半
是德國數學家,他在1937年提出了一個著名的猜想:任給一個正整數n,如果n是偶數,就將它減半![]() 即
即![]() ;如果n是奇數,則將它乘3加
;如果n是奇數,則將它乘3加![]() 即
即![]() ,不斷重復這樣的運算,經過有限步后,一定可以得到
,不斷重復這樣的運算,經過有限步后,一定可以得到![]() 如初始正整數為6,按照上述變換規則,我們得到一個數列:6,3,10,5,16,8,4,2,
如初始正整數為6,按照上述變換規則,我們得到一個數列:6,3,10,5,16,8,4,2,![]() 對科拉茨
對科拉茨![]()
![]() 猜想,目前誰也不能證明,更不能否定
猜想,目前誰也不能證明,更不能否定![]() 現在請你研究:如果對正整數
現在請你研究:如果對正整數![]() 首項
首項![]() 按照上述規則施行變換
按照上述規則施行變換![]() 注:1可以多次出現
注:1可以多次出現![]() 后的第八項為1,則n的所有可能的取值為______.
后的第八項為1,則n的所有可能的取值為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,對于函數
,對于函數![]() 有下述四個結論:
有下述四個結論:
①函數![]() 在其定義域上為增函數;
在其定義域上為增函數;
②對于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且僅有兩個零點;
有且僅有兩個零點;
④若![]() 在點
在點![]() 處的切線也是
處的切線也是![]() 的切線,則
的切線,則![]() 必是
必是![]() 零點.
零點.
其中所有正確的結論序號是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有四個小球,分別寫有“海”“中”“加”“油”四個字,有放回地從中任取一個小球,取到“加”就停止,用隨機模擬的方法估計直到第二次停止的概率:先由計算器產生1到4之間取整數值的隨機數,且用1、2、3、4表示取出小球上分別寫有“海”“中”“加”“油”四個字,以每兩個隨機數為一組,代表兩次的結果.經隨機模擬產生了20組隨機數:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
據此估計,直到第二次就停止概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與直線
與直線![]() 相切且與圓
相切且與圓![]() 外切。
外切。
(1)求圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設第一象限內的點![]() 在軌跡
在軌跡![]() 上,若
上,若![]() 軸上兩點
軸上兩點![]() ,
,![]() ,滿足
,滿足![]() 且
且![]() . 延長
. 延長![]() 、
、![]() 分別交軌跡
分別交軌跡![]() 于
于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 的斜率
的斜率![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調研高中生的作文水平.在某市普通高中的某次聯考中,參考的文科生與理科生人數之比為![]() ,且成績分布在
,且成績分布在![]() 的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中
的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中![]() 構成以2為公比的等比數列.
構成以2為公比的等比數列.
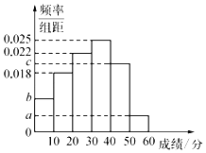
(1)求![]() 的值;
的值;
(2)填寫下面![]() 列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
文科生 | 理科生 | 合計 | |
獲獎 | 6 | ||
不獲獎 | |||
合計 | 400 |
(3)將上述調查所得的頻率視為概率,現從全市參考學生中,任意抽取2名學生,記“獲得優秀作文”的學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附: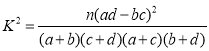 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com