
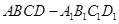 中,底面
中,底面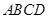 為正方形,
為正方形,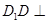 面
面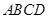 ,
,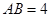 ,
,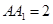 ,點
,點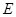 在棱
在棱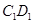 上,且
上,且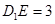 .
.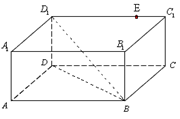
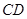 上確定一點
上確定一點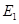 ,使得直線
,使得直線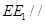 平面
平面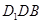 ,并證明;
,并證明;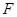 在底面
在底面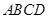 內(nèi),且
內(nèi),且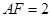 ,請說明點
,請說明點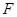 的軌跡,并探求
的軌跡,并探求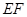 長度的最小值.
長度的最小值.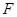 在平面
在平面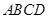 內(nèi)的軌跡是以
內(nèi)的軌跡是以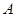 為圓心,半徑等于2的四分之一圓弧,且
為圓心,半徑等于2的四分之一圓弧,且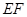 長度的最小值為
長度的最小值為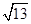 .
.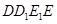 為平行四邊形證明
為平行四邊形證明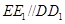 從而證明直線
從而證明直線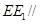 平面
平面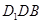 ,或者可以以
,或者可以以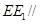 平面
平面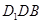 為已知條件出發(fā),利用直線與平面平行的性質(zhì)定理得到
為已知條件出發(fā),利用直線與平面平行的性質(zhì)定理得到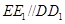 ,進而確定點
,進而確定點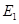 的位置;(Ⅱ)先確定四邊形
的位置;(Ⅱ)先確定四邊形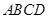 的形狀以及各邊的長度,然后再根據(jù)
的形狀以及各邊的長度,然后再根據(jù)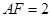 以及點
以及點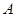 為定點這一條件確定點
為定點這一條件確定點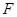 的軌跡,在計算
的軌跡,在計算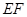 的過程中,可以利用
的過程中,可以利用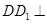 平面
平面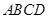 以及
以及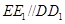 從而得到
從而得到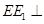 平面
平面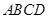 ,于是得到
,于是得到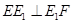 ,進而可以由勾股定理
,進而可以由勾股定理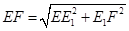 ,從而將問題轉(zhuǎn)化為當
,從而將問題轉(zhuǎn)化為當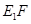 取到最小值時,
取到最小值時,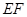 取到最小值.
取到最小值.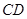 的四等分點
的四等分點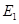 ,使得
,使得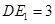 ,則有
,則有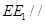 平面
平面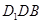 . 證明如下: 1分
. 證明如下: 1分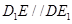 且
且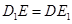 ,
,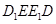 為平行四邊形,則
為平行四邊形,則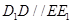 , 2分
, 2分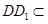 平面
平面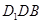 ,
,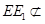 平面
平面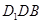 ,所以
,所以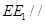 平面
平面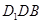 . 4分
. 4分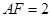 ,所以點
,所以點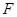 在平面
在平面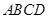 內(nèi)的軌跡是以
內(nèi)的軌跡是以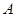 為圓心,半徑等于2的四分之一圓弧. 6分
為圓心,半徑等于2的四分之一圓弧. 6分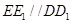 ,
,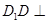 面
面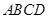 ,所以
,所以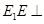 面
面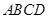 , 7分
, 7分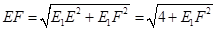 . 8分
. 8分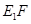 的長度取最小值時,
的長度取最小值時,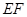 的長度最小,此時點
的長度最小,此時點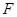 為線段
為線段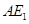 和四分之一圓弧的交點, 10分
和四分之一圓弧的交點, 10分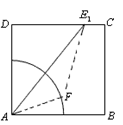
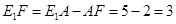 ,
,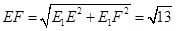 .
.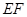 長度的最小值為
長度的最小值為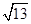 . 12分
. 12分

科目:高中數(shù)學 來源:不詳 題型:解答題
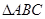 中,
中,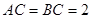 ,
,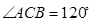 ,
,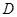 為
為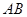 的中點,
的中點,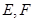 分別在線段
分別在線段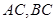 上的動點,且
上的動點,且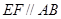 ,
,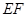 交
交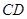 于
于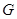 ,把
,把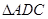 沿
沿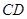 折起,如下圖所示,
折起,如下圖所示,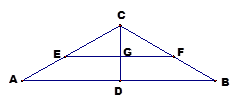
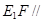 平面
平面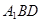 ;
;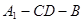 為直二面角時,是否存在點
為直二面角時,是否存在點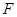 ,使得直線
,使得直線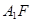 與平面
與平面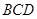 所成的角為
所成的角為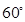 ,若存在求
,若存在求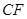 的長,若不存在說明理由。
的長,若不存在說明理由。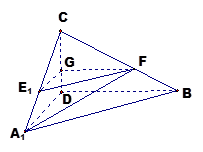
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
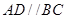 ,
,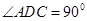 ,平面
,平面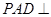 底面
底面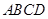 ,
,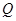 為
為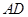 中點,M是棱PC上的點,
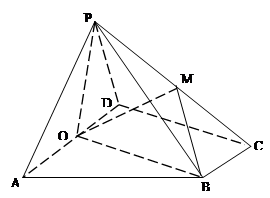
中點,M是棱PC上的點,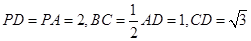 .
.
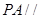 平面
平面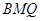 ;
;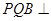 底面
底面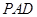 ;
;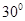 ,設PM=tMC,試確定t的值.
,設PM=tMC,試確定t的值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
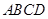 的4個頂點都在球
的4個頂點都在球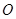 的表面上,
的表面上,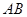 為球
為球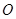 的直徑,
的直徑,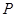 為球面上一點,且
為球面上一點,且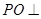 平面
平面 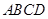 ,
,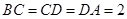 ,點
,點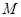 為
為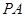 的中點.
的中點. 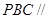 平面
平面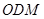 ;
;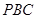 與平面
與平面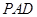 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com