
【題目】已知奇函數 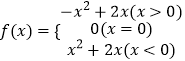
(1)在直角坐標系中畫出y=f(x)的圖象,并指出函數的單調區間;
(2)若函數f(x)在區間[﹣1,a﹣2]上單調遞增,試確定a的取值范圍. 
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,設點
,設點![]() ,且
,且![]() =2.
=2.
(1)求橢圓C的方程;
(2)已知四邊形MNPQ的四個頂點均在曲線C上,且MQ∥NP,MQ⊥x軸,若直線MN和直線QP交于點S(4,0).判斷四邊形MNPQ兩條對角線的交點是否為定點?若是,求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四種說法: ①函數y=ax(a>0且a≠1)與函數y=logaax(a>0且a≠1)的定義域相同;
②函數y=x3與y=3x的值域相同;
③函數y= ![]() +
+ ![]() 與y=
與y= ![]() 都是奇函數;
都是奇函數;
④函數y=(x﹣1)2與y=2x﹣1在區間[0,+∞)上都是增函數.
其中正確的序號是(把你認為正確敘述的序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ;數列
;數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() ,
, ![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)是否存在正整數![]() ,使得
,使得![]() 恰為數列
恰為數列![]() 中的一項?若存在,求所有滿足要求的
中的一項?若存在,求所有滿足要求的![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 的解集中恰有一個元素,求
的解集中恰有一個元素,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某城市氣象部門的數據中,隨機抽取了100天的空氣質量指數的監測數據如表:
空氣質量指數t | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | |
質量等級 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 嚴重污染 |
天數K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)在該城市各醫院每天收治上呼吸道病癥總人數y與當天的空氣質量t(t取整數)存在如下關系y=![]() ,且當t>300時,y>500估計在某一醫院收治此類病癥人數超過200人的概率;
,且當t>300時,y>500估計在某一醫院收治此類病癥人數超過200人的概率;
(2)若在(1)中,當t>300時,y與t的關系擬合于曲線![]() ,現已取出了10對樣本數據(ti,yi)(i=1,2,3,…,10),且
,現已取出了10對樣本數據(ti,yi)(i=1,2,3,…,10),且![]() ,求擬合曲線方程.
,求擬合曲線方程.
(附:線性回歸方程![]() =a+bx中,b=
=a+bx中,b= ,a=
,a=![]() ﹣b
﹣b![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,﹣1),B(4,0),C(2,2),平面區域D是所有滿足 ![]() =λ
=λ ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的點P(x,y)組成的區域.若區域D的面積為4,則ab﹣a﹣b=( )
(1<λ≤a,1<μ≤b)的點P(x,y)組成的區域.若區域D的面積為4,則ab﹣a﹣b=( )
A.﹣1
B.﹣ ![]()
C.![]()
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x(1+m|x|),關于x的不等式f(x)>f(x+m)的解集記為T,若區間[﹣ ![]() ,
, ![]() ]T,則實數m的取值范圍是( )
]T,則實數m的取值范圍是( )
A.( ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣∞, ![]() )
)
D.( ![]() ,0)∪(0,
,0)∪(0, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com