
【題目】已知數集![]() 其中
其中![]() ,
,![]() ,2,
,2,![]() ,n,
,n,![]() ,若對任意的
,若對任意的![]() 2,
2,![]() ,都存在
,都存在![]() ,
,![]() ,使得下列三組向量中恰有一組共線:
,使得下列三組向量中恰有一組共線:
![]() 向量
向量![]() 與向量
與向量![]() ;
;
![]() 向量
向量![]() 與向量
與向量![]() ;
;
![]() 向量
向量![]() 與向量
與向量![]() ,則稱X具有性質P,例如
,則稱X具有性質P,例如![]() 2,
2,![]() 具有性質P.
具有性質P.
![]() 若
若![]() 3,
3,![]() 具有性質P,則x的取值為______
具有性質P,則x的取值為______
![]() 若數集
若數集![]() 3,
3,![]() ,
,![]() 具有性質P,則
具有性質P,則![]() 的最大值與最小值之積為______.
的最大值與最小值之積為______.
【答案】![]() ,
,![]() ,9;
,9; ![]() .
.
【解析】
(1)直接根據性質![]() 的定義,利用向量共線的坐標表示列方程求解即可;(2)由(1)可得
的定義,利用向量共線的坐標表示列方程求解即可;(2)由(1)可得![]() ,
,![]() ,9,當
,9,當![]() 時,具有性質
時,具有性質![]() 的
的![]() ,
,![]() ,
,![]() ,
,![]() ,9,27;
,9,27;![]() 時,具有性質
時,具有性質![]() 的
的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,9;當
,9;當![]() 時,具有性質
時,具有性質![]() 的
的![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,27,81,綜合三種情況可得結果.
,27,81,綜合三種情況可得結果.
![]() 由題意可得:
由題意可得:![]() 與
與![]() ;
;![]() 與
與![]() ;
;![]() 與
與![]() 中恰有一組共線,
中恰有一組共線,
當![]() 與
與![]() 共線時,可得
共線時,可得![]() ,此時另外兩組不共線,符合題意,
,此時另外兩組不共線,符合題意,
當![]() 與
與![]() 共線時,可得
共線時,可得![]() ,此時另外兩組不共線,符合題意,
,此時另外兩組不共線,符合題意,
當![]() 與
與![]() 共線時,可得
共線時,可得![]() ,此時另外兩組不共線,符合題意,
,此時另外兩組不共線,符合題意,
故x的取值為:![]() ,
,![]() ,9;
,9;
![]() 由
由![]() 的求解方法可得
的求解方法可得![]() ,
,![]() ,9,
,9,
當![]() 時,由數集
時,由數集![]() 3,
3,![]() ,
,![]() 具有性質P,
具有性質P,
![]() 若
若![]() 與
與![]() ;
;![]() 與
與![]() ;
;![]() 與
與![]() 中恰有一組共線,可得
中恰有一組共線,可得![]() ,
,![]() ;
;
![]() 若
若![]() 與
與![]() ;
;![]() 與
與![]() ;
;![]() 與
與![]() 中恰有一組共線,可得
中恰有一組共線,可得![]() ,
,![]() ;
;
![]() 若
若![]() 與
與![]() ;
;![]() 與
與![]() ;
;![]() 與
與![]() 中恰有一組共線,可得
中恰有一組共線,可得![]() ,27;
,27;
故![]() 3,
3,![]() ,
,![]() 具有性質P可得
具有性質P可得![]() ,
,![]() ,
,![]() ,
,![]() ,9,27;
,9,27;
同理當![]() 時,
時,![]() 3,
3,![]() ,
,![]() 具有性質P可得
具有性質P可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,9;
,9;
同理當![]() 時,可得
時,可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,27,81;
,27,81;
則![]() 的最大值為90,最小值為
的最大值為90,最小值為![]() ,
,
故![]() 的最大值與最小值之積為
的最大值與最小值之積為![]() .
.
故答案為:![]() ,
,![]() ,9;
,9;![]() .
.


科目:高中數學 來源: 題型:
【題目】為了研究鐘表與三角函數的關系,以9點與3點所在直線為x軸,以6點與12點為y軸,設秒針針尖指向位置P(x,y),若初始位置為P0( ![]() ,
, ![]() ),秒針從P0(注此時t=0)開始沿順時針方向走動,則點P的縱坐標y與時間t(秒)的函數關系為( )
),秒針從P0(注此時t=0)開始沿順時針方向走動,則點P的縱坐標y與時間t(秒)的函數關系為( )
A.y=sin( ![]() t+
t+ ![]() )
)
B.y=sin( ![]() t﹣
t﹣ ![]() )
)
C.y=sin(﹣ ![]() t+
t+ ![]() )
)
D.y=sin(﹣ ![]() t﹣
t﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖在長為10千米的河流![]() 的一側有一條觀光帶,觀光帶的前一部分為曲線段
的一側有一條觀光帶,觀光帶的前一部分為曲線段![]() ,設曲線段
,設曲線段![]() 為函數
為函數![]() (單位:千米)的圖象,且圖象的最高點為
(單位:千米)的圖象,且圖象的最高點為![]() ;觀光帶的后一部分為線段
;觀光帶的后一部分為線段![]() .
.
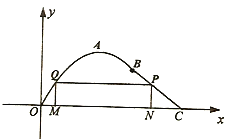
(1)求函數為曲線段![]() 的函數
的函數![]() 的解析式;
的解析式;
(2)若計劃在河流![]() 和觀光帶
和觀光帶![]() 之間新建一個如圖所示的矩形綠化帶
之間新建一個如圖所示的矩形綠化帶![]() ,綠化帶僅由線段
,綠化帶僅由線段![]() 構成,其中點
構成,其中點![]() 在線段
在線段![]() 上.當
上.當![]() 長為多少時,綠化帶的總長度最長?
長為多少時,綠化帶的總長度最長?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的奇函數,且當x≥0時,f(x)=![]() .
.
(1)求f(x)的解析式;
(2)判斷f(x)的單調性;
(3)若對任意的t∈R,不等式f(k-3t2)+f(t2+2t)≤0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】BD是等腰直角三角形△ABC腰AC上的中線,AM⊥BD于點M,延長AM交BC于點N,AF⊥BC于點F,AF與BD交于點E.
(1)求證;△ABE≌△ACN;
(2)求證:∠ADB=∠CDN.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=|x|﹣2|x+3|.
(1)解不等式f(x)≥2;
(2)若存在x∈R使不等式f(x)﹣|3t﹣2|≥0成立,求參數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() +
+ ![]() =1(a>0,b>0)的離心率為
=1(a>0,b>0)的離心率為 ![]() ,其右焦點到直線2ax+by﹣
,其右焦點到直線2ax+by﹣ ![]() =0的距離為
=0的距離為 ![]() .
.
(1)求橢圓C1的方程;
(2)過點P(0,﹣ ![]() )的直線l交橢圓C1于A,B兩點.
)的直線l交橢圓C1于A,B兩點.
①證明:線段AB的中點G恒在橢圓C2: ![]() +
+ ![]() =1的內部;
=1的內部;
②判斷以AB為直徑的圓是否恒過定點?若是,求出該定點的坐標;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com