
【題目】已知正項(xiàng)等比數(shù)列![]() 滿足
滿足![]() ,若存在兩項(xiàng)
,若存在兩項(xiàng)![]() ,使得
,使得![]() ,則
,則![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
設(shè){an}的公比為q(q>0),由等比數(shù)列的通項(xiàng)公式化簡(jiǎn)a7=a6+2a5,求出q,代入aman=16a12化簡(jiǎn)得m,n的關(guān)系式,由“1”的代換和基本不等式求出式子的范圍,驗(yàn)證等號(hào)成立的條件,由m、n的值求出式子的最小值.
設(shè)正項(xiàng)等比數(shù)列{an}的公比為q,且q>0,
由![]() 得:
得:![]() q=
q=![]() +
+![]() ,
,
化簡(jiǎn)得,q2﹣q﹣2=0,解得q=2或q=﹣1(舍去),
因?yàn)?/span>aman=16a12,所以![]() =16a12,
=16a12,
則qm+n﹣2=16,解得m+n=6,
所以![]() =
=![]() (m+n)(
(m+n)(![]() )=
)=![]() (10+
(10+![]() )≥
)≥![]() =
=![]() ,
,
當(dāng)且僅當(dāng)![]() 時(shí)取等號(hào),此時(shí)
時(shí)取等號(hào),此時(shí) ,解得
,解得 ,
,
因?yàn)閙 n取整數(shù),所以均值不等式等號(hào)條件取不到,則![]() >
>![]() ,
,
驗(yàn)證可得,當(dāng)m=2、n=4時(shí),![]() 取最小值為
取最小值為![]() ,
,
故選:B.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() ,且
,且![]() ,則方程
,則方程![]() 在區(qū)間
在區(qū)間![]() 上的所有實(shí)數(shù)根之和最接近下列哪個(gè)數(shù)( )
上的所有實(shí)數(shù)根之和最接近下列哪個(gè)數(shù)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,已知知矩形![]() 中,點(diǎn)
中,點(diǎn)![]() 是邊
是邊![]() 上的點(diǎn),
上的點(diǎn), ![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,且
,且![]() ,現(xiàn)將
,現(xiàn)將![]() 沿
沿![]() 折起,如圖2,點(diǎn)
折起,如圖2,點(diǎn)![]() 的位置記為
的位置記為![]() ,此時(shí)
,此時(shí)![]() .
.


(1)求證: ![]() 面
面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),證明:
時(shí),證明: ![]() ;
;
(2)若關(guān)于![]() 的方程
的方程![]() 有且只有一個(gè)實(shí)根,求實(shí)數(shù)
有且只有一個(gè)實(shí)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 的底面四邊形ABCD為菱形,
的底面四邊形ABCD為菱形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,E為BC的中點(diǎn).
,E為BC的中點(diǎn).

![]() 求證:
求證:![]() 平面PAD;
平面PAD;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() 為自然對(duì)數(shù)的底數(shù),
為自然對(duì)數(shù)的底數(shù), ![]() .
.
(1)試討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),
時(shí), ![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的充分不必要條件,求實(shí)數(shù)
的充分不必要條件,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,“
,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實(shí)數(shù)
”為假命題,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】中歐班列是推進(jìn)與“一帶一路”沿線國(guó)家道路聯(lián)通、貿(mào)易暢通的重要舉措,作為中歐鐵路在東北地區(qū)的始發(fā)站,沈陽(yáng)某火車(chē)站正在不斷建設(shè).目前車(chē)站準(zhǔn)備在某倉(cāng)庫(kù)外,利用其一側(cè)原有墻體,建造一間墻高為3米,底面為12平方米,且背面靠墻的長(zhǎng)方體形狀的保管員室.由于此保管員室的后背靠墻,無(wú)需建造費(fèi)用,因此甲工程隊(duì)給出的報(bào)價(jià)為:屋子前面新建墻體的報(bào)價(jià)為每平方米400元,左右兩面新建墻體報(bào)價(jià)為每平方米150元,屋頂和地面以及其他報(bào)價(jià)共計(jì)7200元.設(shè)屋子的左右兩側(cè)墻的長(zhǎng)度均為![]() 米
米![]() .
.
(1)當(dāng)左右兩面墻的長(zhǎng)度為多少時(shí),甲工程隊(duì)報(bào)價(jià)最低?
(2)現(xiàn)有乙工程隊(duì)也參與此保管員室建造競(jìng)標(biāo),其給出的整體報(bào)價(jià)為![]() 元
元![]() ,若無(wú)論左右兩面墻的長(zhǎng)度為多少米,乙工程隊(duì)都能競(jìng)標(biāo)成功,試求
,若無(wú)論左右兩面墻的長(zhǎng)度為多少米,乙工程隊(duì)都能競(jìng)標(biāo)成功,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() ,
, ![]() ,點(diǎn)
,點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).
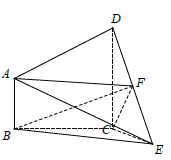
(1)證明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com