
 的等差數列,則|m-n|=
的等差數列,則|m-n|=  是第一個方程的根,代入方程即可求得m,則方程的另一個根可求;設另一個方程的根為s,t,(s≤t)根據韋達定理可知∴s+t=2=
是第一個方程的根,代入方程即可求得m,則方程的另一個根可求;設另一個方程的根為s,t,(s≤t)根據韋達定理可知∴s+t=2= +
+ 根據等差中項的性質可知四個跟成的等差數列為
根據等差中項的性質可知四個跟成的等差數列為 ,s,t,
,s,t, ,進而根據數列的第一項和第四項求得公差,則s和t可求,進而根據韋達定理求得n,最后代入|m-n|即可.
,進而根據數列的第一項和第四項求得公差,則s和t可求,進而根據韋達定理求得n,最后代入|m-n|即可. 是方程①的根,
是方程①的根, 代入方程①,可解得m=
代入方程①,可解得m= ,
, .
. +
+
 ,s,t,
,s,t, ,
, -
- ]÷3=
]÷3= ,
, ,t=
,t= ,
,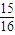
 -
- |=
|= .
.


科目:高中數學 來源:高考數學一輪復習必備(第26課時):第三章 數列-數學鞏固練習(解析版) 題型:選擇題
 的等差數列,則|m-n|等于( )
的等差數列,則|m-n|等于( )


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com