
已知橢圓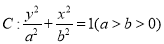 的離心率為
的離心率為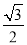 ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線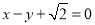 相切.
相切. 是橢圓
是橢圓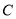 的右頂點與上頂點,直線
的右頂點與上頂點,直線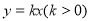 與橢圓相交于
與橢圓相交于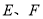 兩點.
兩點.

(1)求橢圓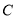 的方程;
的方程;
(2)當四邊形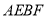 面積取最大值時,求
面積取最大值時,求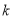 的值.
的值.
(1)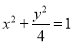 ;(2)2.
;(2)2.
【解析】
試題分析:(1)確定橢圓方程需要兩個獨立條件,首先由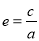 =
=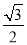 ,得
,得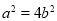 ,其次利用直線和園相切的條件得
,其次利用直線和園相切的條件得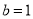 ,從而可求
,從而可求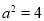 ,進而求得橢圓方程;(2)解析幾何中的最值問題,往往要通過選取變量,將目標函數用一個變量表示,進而轉化為函數的最值問題處理,本題需要將
,進而求得橢圓方程;(2)解析幾何中的最值問題,往往要通過選取變量,將目標函數用一個變量表示,進而轉化為函數的最值問題處理,本題需要將 的面積表示出來,可以表示為
的面積表示出來,可以表示為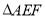 和
和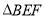 的面積之和,其中
的面積之和,其中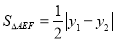 ,
,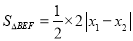 ,將直線
,將直線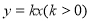 與橢圓聯立,用根與系數的關系將面積用k表示,進而求函數的最大值.
與橢圓聯立,用根與系數的關系將面積用k表示,進而求函數的最大值.
試題解析:(1)由題意知: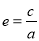 =
=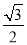 ∴
∴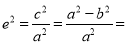
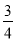 ,∴
,∴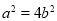 . 2分
. 2分
又∵圓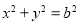 與直線
與直線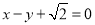 相切, ∴
相切, ∴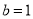 ,∴
,∴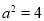 , 3分
, 3分
故所求橢圓C的方程為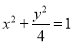 4分
4分
(2)設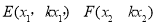 ,其中
,其中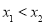 ,
,
將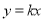 代入橢圓的方程
代入橢圓的方程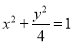 整理得:
整理得: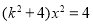 ,
,
故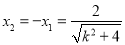 .① 5分
.① 5分
又點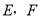 到直線
到直線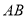 的距離分別為
的距離分別為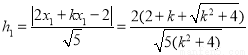 ,
,
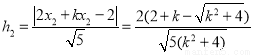 .
.
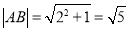 7分
7分
所以四邊形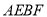 的面積為
的面積為
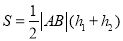
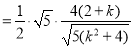
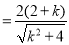 9分
9分
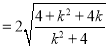


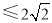 , 11分
, 11分
當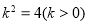 ,即當
,即當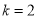 時,上式取等號.
時,上式取等號.
所以當四邊形 面積的最大值時,
面積的最大值時,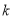 =2. 12分
=2. 12分
考點:1、橢圓的標準方程和簡單幾何性質;2、函數的最值.


科目:高中數學 來源:2015屆廣東省東莞市高二下學期期末理科數學試卷(解析版) 題型:選擇題
用反證法證明命題:“若 是三連續的整數,那么
是三連續的整數,那么 中至少有一個是偶數”時,下列假設正確的是( )
中至少有一個是偶數”時,下列假設正確的是( )
A.假設 中至多有一個偶數
中至多有一個偶數
B.假設 中至多有兩個偶數
中至多有兩個偶數
C.假設 都是偶數
都是偶數
D.假設 都不是偶數
都不是偶數
查看答案和解析>>
科目:高中數學 來源:2015屆山西省忻州市高三上學期第一次四校聯考文科數學試卷(解析版) 題型:填空題
三棱錐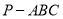 的四個頂點均在同一球面上,其中△
的四個頂點均在同一球面上,其中△ 為等邊三角形,
為等邊三角形,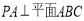 ,
,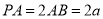 ,則該球的體積是 .
,則該球的體積是 .
查看答案和解析>>
科目:高中數學 來源:2015屆山西省高三10月月考文科數學試卷(解析版) 題型:解答題
(本題小滿分12分)已知數列 是公比大于1的等比數列,a1,a3是函數
是公比大于1的等比數列,a1,a3是函數 的兩個零點.
的兩個零點.
(1)求數列 的通項公式;
的通項公式;
(2)若數列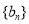 滿足
滿足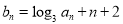 ,且
,且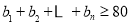 ,求
,求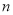 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com