
【題目】已知函數![]() ,
,![]() (e是自然對數的底數),對任意的
(e是自然對數的底數),對任意的![]() R,存在
R,存在![]() ,有
,有![]() ,則
,則![]() 的取值范圍為____________.
的取值范圍為____________.
【答案】![]()
【解析】
問題轉化為f(x)max≤g(x)max,分別求出f(x)和g(x)的最大值,得到關于a的不等式,解出即可.
對任意的x1∈R,存在x2∈[![]() ,2],有f(x1)≤g(x2),
,2],有f(x1)≤g(x2),
故f(x)max≤g(x)max,
f′(x)=![]() ,(x>0),
,(x>0),
令f′(x)>0,解得:0<x<e,
令f′(x)<0,解得:x>e,
故f(x)在(0,e)遞增,在(e,+∞)遞減,
故f(x)max=f(e)=![]() ,
,
g′(x)=﹣2ex+a,
①a≤0時,g′(x)≤0,g(x)在[![]() ,2]遞減,
,2]遞減,
g(x)max=g(![]() )=﹣e
)=﹣e![]() +
+![]() a≥
a≥![]() ,
,
解得:a≥![]() +
+![]() (舍),
(舍),
②a>0時,令g′(x)=0,解得:x=![]() ,
,
(i)![]() ≤
≤![]() 即a≤
即a≤![]() 時,g(x)在[
時,g(x)在[![]() ,2]遞減,
,2]遞減,
結合①,不合題意,舍,
(ii)![]() <
<![]() <2即
<2即![]() <a<4e時,
<a<4e時,
g(x)在[![]() ,
,![]() )遞增,在(
)遞增,在(![]() ,2]遞減,
,2]遞減,
故g(x)max=g(![]() span>)=
span>)=![]() ≥
≥![]() ,
,
解得:a≥2;
(iii)![]() ≥2即a≥4e時,
≥2即a≥4e時,
g(x)在[![]() ,2]遞增,
,2]遞增,
g(x)max=g(2)=﹣4e+2a≥![]() ,
,
解得:a≥2e+![]() ,
,
綜上,a≥2,
故答案為:[2,+∞).


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
【題目】判斷下列全稱量詞命題的真假:
(1)每一個末位是0的整數都是5的倍數;
(2)線段垂直平分線上的點到這條線段兩個端點的距離相等;
(3)對任意負數![]() 的平方是正數;
的平方是正數;
(4)梯形的對角線相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在實數集![]() 上的偶函數
上的偶函數![]() 和奇函數
和奇函數![]() 滿足
滿足![]() .
.
(1)求![]() 與
與![]() 的解析式;
的解析式;
(2)求證:![]() 在區間
在區間![]() 上單調遞增;并求
上單調遞增;并求![]() 在區間
在區間![]() 的反函數;
的反函數;
(3)設![]() (其中
(其中![]() 為常數),若
為常數),若![]() 對于
對于![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在各棱長均為2的正三棱柱![]() 中,
中, ![]() 分別為棱
分別為棱![]() 與
與![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點,其中,
上的動點,其中, ![]() 更靠近
更靠近![]() ,且
,且![]() .
.

(1)證明: ![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月1日為慶祝中華人民共和國成立70周年在北京天安門廣場舉行了盛大的閱兵儀式,共有580臺(套)裝備、160 余架各型飛機接受檢閱。受閱裝備均為中國國產現役主戰裝備,其中包括部分首次公開亮相的新型裝備。例如,在無人機作戰第三方隊中就包括了兩型偵察干擾無人機,可以在遙控設備或自備程序控制操縱的情況下執行任務,進行對敵方通訊設施的電磁壓制和干擾,甚至壓制敵人的防空系統。
某作戰部門對某處的戰場實施“電磁干擾”實驗,據測定,該處的“干擾指數”與無人機干擾源的強度和距離之比成反比,比例系數為常數![]() .現已知相距36km的A. B兩處配置兩架無人機干擾源,其對敵干擾的強度分別為1和
.現已知相距36km的A. B兩處配置兩架無人機干擾源,其對敵干擾的強度分別為1和![]() ,它們連線段上任意一點C處的干擾指數y等于兩機對該處的干擾指數之和,設
,它們連線段上任意一點C處的干擾指數y等于兩機對該處的干擾指數之和,設![]() .
.
(1)試將y表示為x的函數,指出其定義域;
(2)當![]() 時,試確定“干擾指數”最小時C所處位置.
時,試確定“干擾指數”最小時C所處位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足
滿足![]() ,
,![]() ,
,![]() ,
,![]() .s
.s
(1)證明:數列![]() 是等差數列,并求數列
是等差數列,并求數列![]() 的通項;
的通項;
(2)求數列![]() 的通項,并求數列
的通項,并求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,且
,且![]() 是單調遞增數列,求實數
是單調遞增數列,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
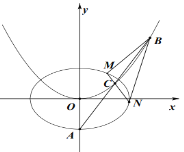
【題目】如圖,![]() 為橢圓
為橢圓![]() 的下頂點.過
的下頂點.過![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 是
是![]() 的中點.
的中點.
(1)求證:點![]() 的縱坐標是定值;
的縱坐標是定值;
(2)過點![]() 作與直線
作與直線![]() 傾斜角互補的直線
傾斜角互補的直線![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點.求
兩點.求![]() 的值,使得
的值,使得![]() 的面積最大.
的面積最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com