
分析 推導出f(x)+f(1-x)=1,從而$f(\frac{1}{2016})+f(\frac{2}{2016})+…+f(\frac{2015}{2016})+f(\frac{2016}{2016})$=1007+f($\frac{1}{2}$)+f(1),由此能求出結(jié)果.
解答 解:∵函數(shù)$f(x)=\frac{3^x}{{{3^x}+\sqrt{3}}}$,
∴f(x)+f(1-x)=$\frac{{3}^{x}}{{3}^{x}+\sqrt{3}}+\frac{{3}^{1-x}}{{3}^{1-x}+\sqrt{3}}$=$\frac{{3}^{x}}{{3}^{x}+1}+\frac{3}{3+\sqrt{3}•{3}^{x}}$=$\frac{{3}^{x}}{{3}^{x}+\sqrt{3}}+\frac{\sqrt{3}}{\sqrt{3}+{3}^{x}}$=1,
∴$f(\frac{1}{2016})+f(\frac{2}{2016})+…+f(\frac{2015}{2016})+f(\frac{2016}{2016})$=1007+f($\frac{1}{2}$)+f(1)
=1007+$\frac{{3}^{\frac{1}{2}}}{{3}^{\frac{1}{2}}+\sqrt{3}}$+$\frac{3}{3+\sqrt{3}}$=1007+$\frac{1}{2}+\frac{3}{2}-\frac{\sqrt{3}}{2}$=1009-$\frac{\sqrt{3}}{2}$.
故答案為:$1009-\frac{{\sqrt{3}}}{2}$.
點評 本題考查函數(shù)值的求法,是基礎題,解題時要認真審題,注意函數(shù)性質(zhì)的合理運用.


 智慧小復習系列答案
智慧小復習系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | f(x)=3-x | B. | f(x)=(x-1)2 | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2+2x |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x2 | C. | y=x-1 | D. | y=x3 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
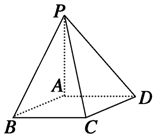
| A. | 平面ABCD | B. | 平面PBC | C. | 平面PAD | D. | 平面PBC |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com