
某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點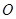 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點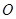 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 ,圓心角為
,圓心角為 (弧度).
(弧度).
(1)求 關于
關于 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為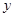 ,求
,求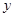 關于
關于 的函數關系式,并求出
的函數關系式,并求出 為何值時,
為何值時, 取得最大值?
取得最大值?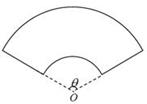
(1)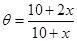 ;(2)
;(2)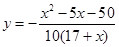 ,當
,當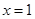 時,花壇的面積與裝飾總費用的比最大.
時,花壇的面積與裝飾總費用的比最大.
解析試題分析:(1)根據已知條件,將周長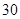 米為等量關系可以建立
米為等量關系可以建立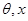 滿足的關系式,再由此關系式進一步得到函數解析式:
滿足的關系式,再由此關系式進一步得到函數解析式: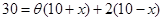 ,即可解得
,即可解得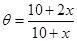 ;(2)根據題意及(1)可得花壇的面積為
;(2)根據題意及(1)可得花壇的面積為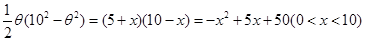 ,裝飾總費用為
,裝飾總費用為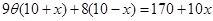 ,因此可得函數解析式
,因此可得函數解析式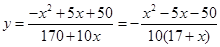 ,而要求
,而要求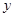 的最大值,即求函數
的最大值,即求函數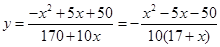 的最大值,可以考慮采用換元法令
的最大值,可以考慮采用換元法令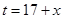 ,從而
,從而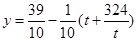 ,再利用基本不等式,即可求得
,再利用基本不等式,即可求得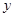 的最大值:
的最大值: ,當且僅當
,當且僅當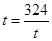 ,
, 時取等號,此時
時取等號,此時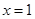 ,
,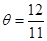 ,因此當
,因此當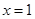 時,花壇的面積與裝飾總費用的比最大.
時,花壇的面積與裝飾總費用的比最大.
試題解析:(1)扇環的圓心角為 ,則
,則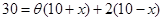 ,∴
,∴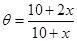 , 3分
, 3分
(2)由(1)可得花壇的面積為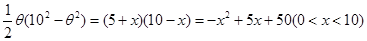 , 6分
, 6分
裝飾總費用為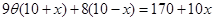 , 8分
, 8分
∴花壇的面積與裝飾總費用的 , 10分
, 10分
令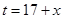 ,則
,則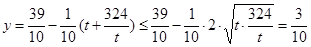 ,當且僅當
,當且僅當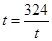 ,
, 時取等號,此時
時取等號,此時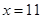 ,
,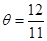 , 12分
, 12分
答:當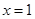 時,花壇的面積與裝飾總費用的比最大. 13分
時,花壇的面積與裝飾總費用的比最大. 13分
考點:1.扇形公式的運用;2.利用基本不等式函數求極值.


科目:高中數學 來源: 題型:解答題
某地上年度電價為0.8元,年用電量為1億千瓦時.本年度計劃將電價調至0.55元~0.75元之間,經測算,若電價調至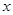 元,則本年度新增用電量
元,則本年度新增用電量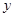 (億千瓦時)與
(億千瓦時)與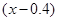 元成反比例.又當
元成反比例.又當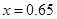 時,
時,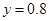 .
.
(1)求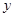 與
與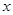 之間的函數關系式;
之間的函數關系式;
(2)若每千瓦時電的成本價為0.3元,則電價調至多少時,本年度電力部門的收益將比上年增加20%?[收益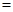 用電量
用電量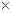 (實際電價-成本價)]
(實際電價-成本價)]
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市環保部門對市中心每天環境污染情況進行調查研究,發現一天中環境污染指數 與時刻
與時刻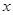 (時)的關系為
(時)的關系為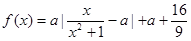 ,
, ,其中
,其中 是與氣象有關的參數,且
是與氣象有關的參數,且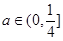 ,用每天
,用每天 的最大值作為當天的污染指數,記作
的最大值作為當天的污染指數,記作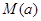 .
.
(1)令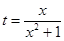 ,
, ,求
,求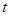 的取值范圍;
的取值范圍;
(2)按規定,每天的污染指數不得超過2,問目前市中心的污染指數是否超標?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
用水清洗一堆蔬菜上殘留的農藥,對用一定量的水清洗一次的效果作如下假定:用一個單位的水可洗掉蔬菜上殘留農藥的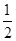 ,用水越多洗掉的農藥量也越多,但總還有農藥殘留在蔬菜上.設用
,用水越多洗掉的農藥量也越多,但總還有農藥殘留在蔬菜上.設用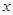 單位量的水清洗一次以后,蔬菜上殘留的農藥量與本次清洗前殘留的農藥量之比為函數
單位量的水清洗一次以后,蔬菜上殘留的農藥量與本次清洗前殘留的農藥量之比為函數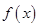 .
.
⑴試規定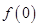 的值,并解釋其實際意義;
的值,并解釋其實際意義;
⑵試根據假定寫出函數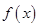 應滿足的條件和具有的性質;
應滿足的條件和具有的性質;
⑶設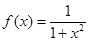 ,現有
,現有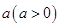 單位量的水,可以清洗一次,也可以把水平均分成兩份后清洗兩次.試問用那種方案清洗后蔬菜上殘留的農藥量比較少?說明理由.
單位量的水,可以清洗一次,也可以把水平均分成兩份后清洗兩次.試問用那種方案清洗后蔬菜上殘留的農藥量比較少?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com