
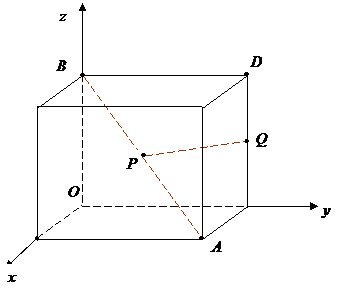
如圖,以正方體的三條棱所在直線為坐標(biāo)軸,建立空間直角坐標(biāo)系![]() .點(diǎn)
.點(diǎn)![]() 在正方體的對(duì)角線
在正方體的對(duì)角線![]() 上,點(diǎn)
上,點(diǎn)![]() 在正方體的棱
在正方體的棱![]() 上.
上.
當(dāng)點(diǎn)![]() 為對(duì)角線
為對(duì)角線![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在棱
在棱![]() 上運(yùn)動(dòng)時(shí),探究
上運(yùn)動(dòng)時(shí),探究![]() 的最小值;
的最小值;
當(dāng)點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在對(duì)角線
在對(duì)角線![]() 上運(yùn)動(dòng)時(shí),探究
上運(yùn)動(dòng)時(shí),探究![]() 的最小值;
的最小值;
當(dāng)點(diǎn)![]() 在對(duì)角線
在對(duì)角線![]() 上運(yùn)動(dòng),點(diǎn)
上運(yùn)動(dòng),點(diǎn)![]() 在棱
在棱![]() 上運(yùn)動(dòng)時(shí),探究
上運(yùn)動(dòng)時(shí),探究![]() 的最小值.
的最小值.
由以上問題,你得到了什么結(jié)論?你能證明你的結(jié)論嗎?
(1)![]() 有最小值
有最小值![]() (2)
(2)![]() 取得最小值
取得最小值![]() (3)最小值是
(3)最小值是![]()
設(shè)正方體的棱長(zhǎng)為![]() .
.
當(dāng)點(diǎn)![]() 為對(duì)角線
為對(duì)角線![]() 的中點(diǎn)時(shí),點(diǎn)
的中點(diǎn)時(shí),點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() .
.
因?yàn)辄c(diǎn)![]() 在線段
在線段![]() 上,設(shè)
上,設(shè)![]() .
.
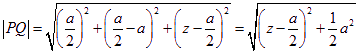 .
.
當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為
的最小值為![]() ,即點(diǎn)
,即點(diǎn)![]() 在棱
在棱![]() 的中點(diǎn)時(shí),
的中點(diǎn)時(shí),![]() 有最小值
有最小值![]() .
.
因?yàn)?img width=16 height=17 src="http://thumb.zyjl.cn/pic1/1899/sx/197/50997.gif">在對(duì)角線![]() 上運(yùn)動(dòng).
上運(yùn)動(dòng).![]() 是定點(diǎn),所以當(dāng)
是定點(diǎn),所以當(dāng)
![]() 時(shí),
時(shí),![]() 最短.因?yàn)楫?dāng)點(diǎn)
最短.因?yàn)楫?dāng)點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn)時(shí),
的中點(diǎn)時(shí),![]() ,
,![]() 是等腰三角形,所以,當(dāng)點(diǎn)
是等腰三角形,所以,當(dāng)點(diǎn)![]() 是
是![]() 的中點(diǎn)時(shí),
的中點(diǎn)時(shí),![]() 取得最小值
取得最小值![]() .
.
當(dāng)點(diǎn)![]() 在對(duì)角線
在對(duì)角線![]() 上運(yùn)動(dòng),點(diǎn)
上運(yùn)動(dòng),點(diǎn)![]() 在棱
在棱![]() 上運(yùn)動(dòng)
上運(yùn)動(dòng)
時(shí),![]() 的最小值仍然是
的最小值仍然是![]() .
.
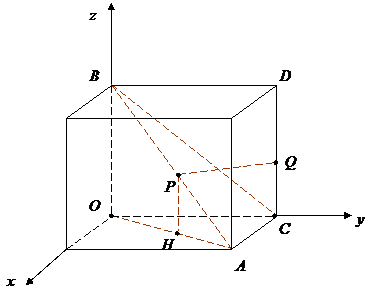
證明:如下圖,設(shè)![]() ,由正方體的對(duì)稱性,顯然有
,由正方體的對(duì)稱性,顯然有![]() .
.
設(shè)![]() 在平面
在平面![]() 上的射影是
上的射影是![]() .在
.在![]() 中,
中,![]() ,所以
,所以![]() ,即有
,即有![]() .
.
所以,點(diǎn)![]() 的坐標(biāo)是
的坐標(biāo)是![]() .
.
由已知,可設(shè)![]() ,則
,則
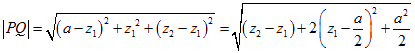 .
.
當(dāng)![]() 時(shí),
時(shí),![]() 取得最小值,最小值是
取得最小值,最小值是![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:044
如圖
,以正方體的三條棱所在直線為坐標(biāo)軸,建立空間直角坐標(biāo)系O-xyz,點(diǎn)P在正方體的對(duì)角線AB上,點(diǎn)Q在正方體的棱CD上.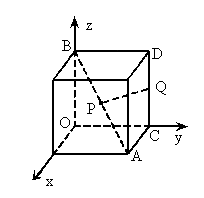
(1)
當(dāng)點(diǎn)P為對(duì)角線AB的中點(diǎn),點(diǎn)Q在棱CD上運(yùn)動(dòng)時(shí),探究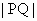 的最小值;
的最小值;
(2)
當(dāng)點(diǎn)Q為棱CD的中點(diǎn),點(diǎn)P在對(duì)角線AB上運(yùn)動(dòng)時(shí),探究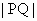 的最小值;
的最小值;
(3)
當(dāng)點(diǎn)P在對(duì)角線AB上運(yùn)動(dòng),點(diǎn)Q在棱CD上運(yùn)動(dòng)時(shí),探究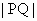 的最小值.
的最小值.
由以上問題,你得到了什么結(jié)論,你能證明你的結(jié)論嗎?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:高考總復(fù)習(xí)全解 數(shù)學(xué) 一輪復(fù)習(xí)·必修課程 (人教實(shí)驗(yàn)版) B版 人教實(shí)驗(yàn)版 B版 題型:044
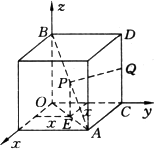
如圖,以正方體的三條棱所在直線為坐標(biāo)軸,建立空間直角坐標(biāo)系O-xyz,點(diǎn)P在對(duì)角線AB上運(yùn)動(dòng),點(diǎn)Q為棱CD的中點(diǎn),探求|PQ|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:數(shù)學(xué)教研室 題型:044
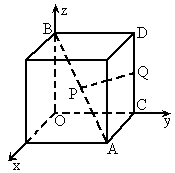
如圖,以正方體的三條棱所在直線為坐標(biāo)軸,建立空間直角坐標(biāo)系O-xyz,點(diǎn)P在正方體的對(duì)角線AB上,點(diǎn)Q在正方體的棱CD上.
(1)當(dāng)點(diǎn)P為對(duì)角線AB的中點(diǎn),點(diǎn)在Q在棱CD上運(yùn)動(dòng)時(shí),探究|PQ|的最小值;
(2)當(dāng)點(diǎn)Q為棱CD的中點(diǎn),點(diǎn)P在對(duì)角線上運(yùn)動(dòng)時(shí),探究|PQ|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年湖北省高二期中考試文科數(shù)學(xué)試卷 題型:解答題
(本小題滿分12分)如圖在棱長(zhǎng)為1正方體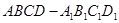 中,以正方體的三條棱所在直線為軸建立空間直角坐標(biāo)系
中,以正方體的三條棱所在直線為軸建立空間直角坐標(biāo)系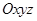 ,
,
(I)若點(diǎn)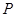 在線段
在線段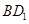 上,且滿足
上,且滿足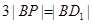 ,試寫出點(diǎn)
,試寫出點(diǎn)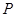 的坐標(biāo)并寫出
的坐標(biāo)并寫出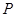 關(guān)于平面
關(guān)于平面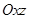 的對(duì)稱點(diǎn)
的對(duì)稱點(diǎn)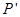 的坐標(biāo);
的坐標(biāo);
(Ⅱ)線段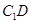 中點(diǎn)為
中點(diǎn)為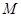 ,求點(diǎn)
,求點(diǎn)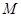 到點(diǎn)
到點(diǎn)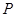 的距離。
的距離。
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com