
分析 (1)利用函數(shù)y=Asin(ωx+φ)的圖象變換規(guī)律求得g(x)的解析式,再利用正弦函數(shù)的單調(diào)性,求得g(x)的單調(diào)增區(qū)間.
(2)利用正弦函數(shù)的零點(diǎn)和周期性,求得n-m的最小值.
解答 解:(1)把函數(shù)f(x)=2sin2x 的圖象向左平移$\frac{π}{6}$個(gè)單位,可得y=2sin(2x+$\frac{π}{3}$)的圖象;
再向上平移1個(gè)單位,得到函數(shù)y=g(x)=2sin(2x+$\frac{π}{3}$)+1的圖象.
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{6}$,可得g(x)的單調(diào)增區(qū)間為[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{6}$,],k∈Z.
(2)令g(x)=2sin(2x+$\frac{π}{3}$)+1=0,求得sin(2x+$\frac{π}{3}$)=-$\frac{1}{2}$,∴2x+$\frac{π}{3}$=2kπ-$\frac{2π}{3}$,或2x+$\frac{π}{3}$=2kπ-$\frac{π}{3}$,
即x=kπ-$\frac{π}{2}$,或 x=kπ-$\frac{π}{3}$,k∈Z.
故函數(shù)g(x)在一個(gè)周期上有兩個(gè)零點(diǎn).
根據(jù)y=g(x)在[m,n]上至少含有30個(gè)零點(diǎn),在所有滿足上述條件的[m,n]中,
當(dāng)n-m的最小值時(shí),可取m=-$\frac{π}{2}$,n=14π-$\frac{π}{3}$,此時(shí),n-m=14π+$\frac{π}{6}$=$\frac{85π}{6}$.
點(diǎn)評(píng) 本題主要考查函數(shù)y=Asin(ωx+φ)的圖象變換規(guī)律,正弦函數(shù)的單調(diào)性、零點(diǎn)和周期性,屬于中檔題.


 優(yōu)等生題庫(kù)系列答案
優(yōu)等生題庫(kù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
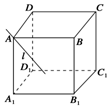 如圖所示,過(guò)正方體ABCD-A1B1C1D1的頂點(diǎn)A作直線l,使l與棱AB,AD,AA1所成的角都相等,這樣的直線l可以作4條.
如圖所示,過(guò)正方體ABCD-A1B1C1D1的頂點(diǎn)A作直線l,使l與棱AB,AD,AA1所成的角都相等,這樣的直線l可以作4條.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com