
【題目】已知函數![]() .
.
(I) 求![]() 極大值;
極大值;
(II) 求證:![]() ,其中
,其中![]() ,
, ![]() .
.
(III)若方程![]() 有兩個不同的根
有兩個不同的根![]() , 求證:
, 求證: ![]()
【答案】(Ⅰ)極大值是![]() (II)見解析(III)見解析
(II)見解析(III)見解析
【解析】
(Ⅰ)對函數進行求導,讓導函數為零,求出根,列表,判斷極值情況,最后求出![]() 極大值;
極大值;
(II) 法一:根據(Ⅰ)可以得到函數的最大值,結合求證的式子左右兩邊形式,能得到一個不等式, 然后累和,命題得證;
法二:有關正整數![]() 的命題,可以采用數學歸納法來證明。
的命題,可以采用數學歸納法來證明。
(III)由(Ⅰ)可知,方程![]() 有兩個不同的零點
有兩個不同的零點![]() ,能得到
,能得到![]()
![]() 用分析法證明時,需要構造一個新函數,利用新函數的單調性,證明分析法需要證明的不等式成立。
用分析法證明時,需要構造一個新函數,利用新函數的單調性,證明分析法需要證明的不等式成立。
解:(Ⅰ)![]() , 解得
, 解得![]()
|
|
|
|
|
|
|
|
| 遞增 | 極大值 | 遞減 |
![]() 極大值是
極大值是![]()
(II) 法一:![]() ,
,
由(Ⅰ)得:![]() 在
在![]() 處取得極大值1,且該極值是唯一的,
處取得極大值1,且該極值是唯一的,
則![]() ,即
,即![]() ,當且僅當
,當且僅當![]() 時取“=”,
時取“=”,
故當![]() 時,
時,![]() ,
,
因此![]() .
.
法二:下面用數學歸納法證明:![]() ,對
,對![]() 恒成立.
恒成立.
(1)當![]() 時,左邊
時,左邊![]() ,右邊
,右邊![]() ,
,
左邊![]() 右邊,結論成立;
右邊,結論成立;
(2)假設當![]() 時,結論成立,即
時,結論成立,即![]() ,
,
當![]() 時,左邊
時,左邊![]()
![]() ,
,
而![]()
![]() ,
,
![]() ,
,
由(Ⅰ)得:![]() 在
在![]() 處取得極大值1,且該極值是唯一的,
處取得極大值1,且該極值是唯一的,
則![]() ,即
,即![]() ,當且僅當
,當且僅當![]() 時取“=”,
時取“=”,
則![]() 對
對![]() 恒成立,即
恒成立,即
![]() 成立
成立
故當![]() 時,結論成立,
時,結論成立,
因此,綜合(1)(2)得![]() ,對
,對![]() 恒成立
恒成立
(III) 由(Ⅰ)知方程![]() 有兩個不同的零點
有兩個不同的零點![]() ,
,
則![]()
![]()
分析法: 要證![]()
![]()
![]()
![]()
![]()
令函數![]() ,
, ![]()
由![]() 得
得
![]() 在
在![]() 上遞增,
上遞增, ![]()
即![]() 成立, 由上知
成立, 由上知![]() 成立.
成立.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點(如圖所示),點
的左、右頂點(如圖所示),點![]() 在橢圓的長軸
在橢圓的長軸![]() 上運動,且
上運動,且![]() .設圓
.設圓![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓.
為半徑的圓.
(1)若![]() ,圓
,圓![]() 和橢圓在第一象限的交點坐標為
和橢圓在第一象限的交點坐標為![]() ,求橢圓的方程;
,求橢圓的方程;
(2)若橢圓的離心率為![]() ,過點
,過點![]() 作互相垂直的兩條直線,交橢圓于P,Q兩點,若直線PQ過點M,求m的值(用含
作互相垂直的兩條直線,交橢圓于P,Q兩點,若直線PQ過點M,求m的值(用含![]() 的代數式表示);
的代數式表示);
(3)當圓![]() 與橢圓有且僅有點
與橢圓有且僅有點![]() 一個交點時,求
一個交點時,求![]() 的運動范圍(用含
的運動范圍(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明家的晚報在下午![]() 任何一個時間隨機地被送到,他們一家人在下午
任何一個時間隨機地被送到,他們一家人在下午![]() 任何一個時間隨機地開始晚餐.為了計算晚報在晚餐開始之前被送到的概率,某小組借助隨機數表的模擬方法來計算概率,他們的具體做法是將每個1分鐘的時間段看作個體進行編號,
任何一個時間隨機地開始晚餐.為了計算晚報在晚餐開始之前被送到的概率,某小組借助隨機數表的模擬方法來計算概率,他們的具體做法是將每個1分鐘的時間段看作個體進行編號,![]() 編號為01,
編號為01,![]() 編號為02,依此類推,
編號為02,依此類推,![]() 編號為90.在隨機數表中每次選取一個四位數,前兩位表示晚報時間,后兩位表示晚餐時間,如果讀取的四位數表示的晚報晚餐時間有一個不符合實際意義,視為這次讀取的無效數據(例如下表中的第一個四位數7840中的78不符合晚報時間).按照從左向右,讀完第一行,再從左向右讀第二行的順序,讀完下表,用頻率估計晚報在晚餐開始之前被送到的概率為
編號為90.在隨機數表中每次選取一個四位數,前兩位表示晚報時間,后兩位表示晚餐時間,如果讀取的四位數表示的晚報晚餐時間有一個不符合實際意義,視為這次讀取的無效數據(例如下表中的第一個四位數7840中的78不符合晚報時間).按照從左向右,讀完第一行,再從左向右讀第二行的順序,讀完下表,用頻率估計晚報在晚餐開始之前被送到的概率為![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() ,若
,若![]() ,則對此不等式描敘正
,則對此不等式描敘正
確的是( )
A. 若![]() ,則至少存在一個以
,則至少存在一個以![]() 為邊長的等邊三角形
為邊長的等邊三角形
B. 若![]() ,則對任意滿足不等式的
,則對任意滿足不等式的![]() 都存在以
都存在以![]() 為邊長的三角形
為邊長的三角形
C. 若![]() ,則對任意滿足不等式的
,則對任意滿足不等式的![]() 都存在以
都存在以![]() 為邊長的三角形
為邊長的三角形
D. 若![]() ,則對滿足不等式的
,則對滿足不等式的![]() 不存在以
不存在以![]() 為邊長的直角三角形
為邊長的直角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新鮮的荔枝很好吃,但摘下后容易變黑,影響賣相.某大型超市進行扶貧工作,按計劃每年六月從精準扶貧戶中訂購荔枝,每天進貨量相同且每公斤20元,售價為每公斤24元,未售完的荔枝降價處理,以每公斤16元的價格當天全部處理完.根據往年情況,每天需求量與當天平均氣溫有關.如果平均氣溫不低于25攝氏度,需求量為![]() 公斤;如果平均氣溫位于
公斤;如果平均氣溫位于![]() 攝氏度,需求量為
攝氏度,需求量為![]() 公斤;如果平均氣溫位于
公斤;如果平均氣溫位于![]() 攝氏度,需求量為
攝氏度,需求量為![]() 公斤;如果平均氣溫低于15攝氏度,需求量為
公斤;如果平均氣溫低于15攝氏度,需求量為![]() 公斤.為了確定6月1日到30日的訂購數量,統計了前三年6月1日到30日各天的平均氣溫數據,得到如圖所示的頻數分布表:
公斤.為了確定6月1日到30日的訂購數量,統計了前三年6月1日到30日各天的平均氣溫數據,得到如圖所示的頻數分布表:
平均氣溫 |
|
|
|
|
|
|
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
(Ⅰ)假設該商場在這90天內每天進貨100公斤,求這90天荔枝每天為該商場帶來的平均利潤(結果取整數);
(Ⅱ)若該商場每天進貨量為200公斤,以這90天記錄的各需求量的頻率作為各需求量發生的概率,求當天該商場不虧損的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
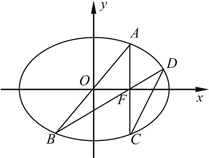
【題目】如圖,在平面直角坐標系xOy中,已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
. ![]() 為橢圓的右焦點,
為橢圓的右焦點, ![]() 為橢圓上關于原點對稱的兩點,連接
為橢圓上關于原點對稱的兩點,連接![]() 分別交橢圓于
分別交橢圓于![]() 兩點.
兩點.
⑴求橢圓的標準方程;
⑵若![]() ,求
,求![]() 的值;
的值;
⑶設直線![]() ,
, ![]() 的斜率分別為
的斜率分別為![]() ,
, ![]() ,是否存在實數
,是否存在實數![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com