

分析 (Ⅰ)由已知可得BC∥AE,再由BF⊥BC,得BF⊥AE,進一步得到∠PFB為二面角P-AE-C的平面角為60°,在△BFP中,利用余弦定理求得BP;
(Ⅱ)由勾股定理可知BF⊥PB,再由線面垂直的判定和性質可得AE⊥PB,則有PB⊥平面ABCE;
(Ⅲ)法一、作BN⊥PF于N點,連AN,由(Ⅱ)可知,AE⊥面BFP,得面BFP⊥面APE,進一步可得BN⊥面APE,則∠BAN是直線AB與平面APE所成的角,求解三角形得答案;
法二、由于BF,BP,BC兩兩互相垂直,如圖,建立空間直角坐標系,求出所用點的坐標,得到平面APE的一個法向量$\overrightarrow{n}$,再求出$\overrightarrow{AB}$的坐標,由向量$\overrightarrow{n}$與$\overrightarrow{AB}$所成角的余弦值可得直線CE與平面APE所成角的正弦值.
解答 解:(Ⅰ)∵AB∥EC,AB=EC,∴四邊形ABCE是平行四邊形,則BC∥AE,
又∵BF⊥BC,∴BF⊥AE,
∴AE⊥FB,AE⊥FP,即∠PFB為二面角P-AE-C的平面角為60°,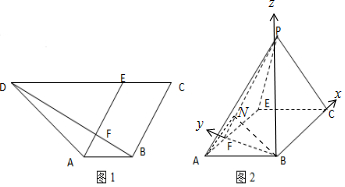
又$BF=\sqrt{3},PF=2\sqrt{3}$,由余弦定理BP2=BF2+PF2-2BF•PFcos∠BFP=9,
得BP=3;
證明:(Ⅱ)∵$BF=\sqrt{3},PF=2\sqrt{3}$,
BP=3,滿足BF2+BP2=PF2,∴BF⊥PB.
又∵BF⊥AE,PF⊥AE,且BF∩PF=F,
∴AE⊥面PFB,則AE⊥PB,
而BF∩AE=F,∴PB⊥平面ABCE;
解:(Ⅲ)法一、作BN⊥PF于N點,連AN,
由(Ⅱ)可知,AE⊥面BFP,∴面BFP⊥面APE,
又面BFP∩面APE=PF,∴BN⊥面APE,則∠BAN是直線AB與平面APE所成的角.
在直角三角形FBP中,BN=BF•sin60°=$\frac{3}{2}$,∴sin∠NAB=$\frac{BN}{AB}$=$\frac{\frac{3}{2}}{2}=\frac{3}{4}$.
∴直線AB與平面APE所成角的正弦值為$\frac{3}{4}$.
∵AB∥CE,
∴直線CE與平面APE所成角的正弦值為$\frac{3}{4}$;
法二、由于BF,BP,BC兩兩互相垂直,如圖,建立空間直角坐標系,
則$B(0,0,0),C(3,0,0),A(-1,\sqrt{3},0),E(2,\sqrt{3},0),P(0,0,3)$,
設平面APE的法向量為$\overrightarrow n=(x,y,z)$,
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AE}=0}\\{\overrightarrow n•\overrightarrow{AP}=0}\end{array}}\right.$,得$\left\{{\begin{array}{l}{(x,y,z)•(3,0,0)=0}\\{(x,y,z)•(1,-\sqrt{3},3)=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{x=0}\\{x-\sqrt{3}y+3z=0}\end{array}}\right.$,取z=1,得$\overrightarrow n=(0,\sqrt{3},1)$,
設直線AB與平面APE所成的角為θ,$\overrightarrow{AB}=(1,-\sqrt{3},0)$,
則sinθ=|cos<$\overrightarrow{n},\overrightarrow{AB}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{AB}|}{|\overrightarrow{n}|•|\overrightarrow{AB}|}=\frac{|-3|}{2×2}=\frac{3}{4}$,
故直線AB與平面APE所成角的正弦值為$\frac{3}{4}$,
∵AB∥CE,
∴直線CE與平面APE所成角的正弦值為$\frac{3}{4}$.
點評 本題考查直線與平面垂直的判定,考查空間想象能力和思維能力,訓練了利用空間向量求解線面角,是中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2017屆湖北省協作校高三聯考一數學(理)試卷(解析版) 題型:選擇題
已知命題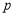 :對任意
:對任意 ,
,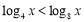 ,命題
,命題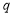 :存在
:存在 ,使得
,使得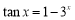 ,則下列命題為真命題的是( )
,則下列命題為真命題的是( )
A.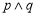 B.
B.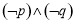
C.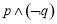 D.
D.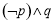
查看答案和解析>>
科目:高中數學 來源:2016-2017學年重慶市高一上學期第一次月考數學試卷(解析版) 題型:選擇題
已知二次函數 (
( )的圖象如圖所示,在下列結論中:①
)的圖象如圖所示,在下列結論中:① ;②
;② ;③b=-2a;④
;③b=-2a;④ ,正確結論的個數是( )
,正確結論的個數是( )

A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向左平移$\frac{π}{4}$個單位長度,再把所得各點的橫坐標縮短到原來的$\frac{1}{3}$倍 (縱坐標不變) | |
| B. | 向右平移$\frac{π}{4}$個單位長度,再把所得各點的橫坐標縮短到原來的$\frac{1}{3}$倍(縱坐標不變) | |
| C. | 向左平移$\frac{π}{4}$個單位長度,再把所得各點的橫坐標伸長到原來的3倍(縱坐標不變) | |
| D. | 向右平移$\frac{π}{4}$個單位長度,再把所得各點的橫坐標伸長到原來的3倍(縱坐標不變) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 35種 | B. | 70種 | C. | 210種 | D. | 105種 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com