
【題目】已知函數![]()
![]()
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)證明:![]() .
.
【答案】(1)![]() (2)詳見解析
(2)詳見解析
【解析】
試題分析:(1)利用導數幾何意義得:曲線![]() 在
在![]() 處的切線斜率等于該點處導數值,k=f′(1)=e,而f(1)=2,利用點斜式得切線方程為
處的切線斜率等于該點處導數值,k=f′(1)=e,而f(1)=2,利用點斜式得切線方程為![]() (2)先調整所證不等式:
(2)先調整所證不等式:![]() 等價于
等價于![]() ,再利用導數分別研究左右函數最值:設函數g(x)=xln x,g(x)在(0,+∞)上的最小值為g
,再利用導數分別研究左右函數最值:設函數g(x)=xln x,g(x)在(0,+∞)上的最小值為g![]() =-
=-![]() ;設函數h(x)=xe-x-
;設函數h(x)=xe-x-![]() ,則h(x)在(0,+∞)上的最大值為h(1)=-
,則h(x)在(0,+∞)上的最大值為h(1)=-![]() .但兩個函數取最值時的自變量不同,因此等于號取不到,從而得證.
.但兩個函數取最值時的自變量不同,因此等于號取不到,從而得證.
試題解析:解:(1)函數f(x)的定義域為(0,+∞),
![]()
由題意可得f(1)=2,f′(1)=e,故曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ;
;
(2)證明:由(1)知,f(x)=exln x+![]() ex-1,
ex-1,
從而![]() 等價于
等價于![]() .
.
設函數g(x)=xln x,
則g′(x)=1+ln x,
所以當x∈![]() 時,g′(x)<0;
時,g′(x)<0;
當x∈![]() 時,g′(x)>0.
時,g′(x)>0.
故g(x)在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,從而g(x)在(0,+∞)上的最小值為
上單調遞增,從而g(x)在(0,+∞)上的最小值為
g![]() =-
=-![]() .
.
設函數h(x)=xe-x-![]() ,則h′(x)=e-x(1-x).
,則h′(x)=e-x(1-x).
所以當x∈(0,1)時,h′(x)>0;
當x∈(1,+∞)時,h′(x)<0.
故h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,從而h(x)在(0,+∞)上的最大值為
h(1)=-![]() .
.
因為gmin(x)=g![]() =h(1)=hmax(x),
=h(1)=hmax(x),
所以當x>0時,g(x)>h(x),即f(x)>1.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案科目:高中數學 來源: 題型:
【題目】調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業者崗位分布條形圖,則下列結論中不一定正確的是( )

A. 互聯網行業從業人員中90后占一半以上
B. 互聯網行業中從事技術崗位的人數超過總人數的![]()
C. 互聯網行業中從事運營崗位的人數90后比80前多
D. 互聯網行業中從事運營崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校統計了本校高一年級學生期中考試的數學成績,其數學成績(滿分150分)均在![]() 內,將這些成績分成
內,將這些成績分成![]() 5組,得到如圖所示的頻率分布直方圖.
5組,得到如圖所示的頻率分布直方圖.
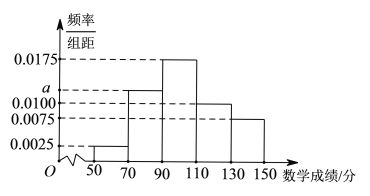
(1)求a的值;
(2)求該校高一年級學生期中考試的數學成績的中位數(結果保留一位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了反映國民經濟各行業對倉儲物流業務的需求變化情況,以及重要商品庫存變化的動向,中國物流與采購聯合會和中儲發展股份有限公司通過聯合調查,制定了中國倉儲指數.如圖所示的折線圖是2016年1月至2017年12月的中國倉儲指數走勢情況.

根據該折線圖,下列結論正確的是
A. 2016年各月的倉儲指數最大值是在3月份
B. 2017年1月至12月的倉儲指數的中位數為54%
C. 2017年1月至4月的倉儲指數比2016年同期波動性更大
D. 2017年11月的倉儲指數較上月有所回落,顯示出倉儲業務活動仍然較為活躍,經濟運行穩中向好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,以極軸為
,以極點為原點,以極軸為![]() 軸的正半軸,取相同的單位長度,建立平面直角坐標系,直線
軸的正半軸,取相同的單位長度,建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為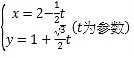 .
.
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 經過伸縮變換
經過伸縮變換![]() 得到曲線
得到曲線![]() ,曲線
,曲線![]() 上任一點為
上任一點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() 、
、![]() ,
,![]() 為橢圓
為橢圓![]() 的一個短軸頂點,
的一個短軸頂點,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若經過橢圓![]() 左焦點的直線
左焦點的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 為橢圓
為橢圓![]() 的右頂點,求
的右頂點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知球O是正三棱錐(底面為正三角形,頂點在底面的射影為底面中心)A-BCD的外接球,BC=3,![]() ,點E在線段BD上,且BD=3BE,過點E作圓O的截面,則所得截面圓面積的取值范圍是__.
,點E在線段BD上,且BD=3BE,過點E作圓O的截面,則所得截面圓面積的取值范圍是__.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班“數學興趣小組”對函數y=﹣x2+2|x|+1的圖象和性質進行了探究,探究過程如下,請補充完整.
(1)自變量x的取值范圍是全體實數,x與y的幾組對應值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,畫出了函數圖象的一部分,請畫出該函數圖象的另一部分.
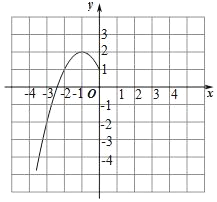
(3)觀察函數圖象,寫出兩條函數的性質./p>
(4)進一步探究函數圖象發現:
①方程﹣x2+2|x|+1=0有 個實數根;
②關于x的方程﹣x2+2|x|+1=a有4個實數根時,a的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com