
【題目】已知函數![]() .
.
(1)求函數![]() 的最小正周期及單調增區間;
的最小正周期及單調增區間;
(2)當![]() 時,求函數
時,求函數![]() 的最大值及最小值.
的最大值及最小值.
【答案】(1)周期![]() ,增區間為
,增區間為![]() (2)最大值為
(2)最大值為![]() ,最小值為-1
,最小值為-1
【解析】
(1)找出函數f(x)解析式中的ω的值,代入周期公式即可求出函數的最小正周期,由正弦函數的單調遞增區間[2kπ![]() ,2kπ
,2kπ![]() ]列出關于x的不等式,求出不等式的解集即為函數的單調遞增區間;
]列出關于x的不等式,求出不等式的解集即為函數的單調遞增區間;
(2)由x的范圍,求出2x![]() 的范圍,根據正弦函數的圖象與性質可得2x
的范圍,根據正弦函數的圖象與性質可得2x![]() 為
為![]() 時,f(x)取得最大值,當2x
時,f(x)取得最大值,當2x![]() 為
為![]() 時函數f(x)取得最小值,分別求出最大值和最小值即可.
時函數f(x)取得最小值,分別求出最大值和最小值即可.
(1)f(x)![]() sin(2x
sin(2x![]() ),
),
∵ω=2,∴最小正周期T![]() π,由2kπ
π,由2kπ![]() 2x
2x![]() 2kπ
2kπ![]() (k∈Z),
(k∈Z),
解得kπ![]() x≤kπ
x≤kπ![]() (k∈Z),
(k∈Z),
故函數f(x)的單調增區間是[kπ![]() ,kπ
,kπ![]() ](k∈Z);
](k∈Z);
(2)當x∈[![]() ,
,![]() ]時,(2x
]時,(2x![]() )∈[
)∈[![]() ,
,![]() ],
],
故當2x![]() ,即x
,即x![]() 時,f(x)有最大值
時,f(x)有最大值![]() ,
,
當2x![]() ,即x
,即x![]() 時,f(x)有最小值﹣1.
時,f(x)有最小值﹣1.


 星級口算天天練系列答案
星級口算天天練系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,且a2=2b.
,且a2=2b.
(1)求橢圓的方程;
(2)直線l:x﹣y+m=0與橢圓交于A,B兩點,是否存在實數m,使線段AB的中點在圓x2+y2=5上,若存在,求出m的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數 ,下列
,下列![]() 個結論正確的是__________(把你認為正確的答案全部寫上).
個結論正確的是__________(把你認為正確的答案全部寫上).
(1)任取![]() ,都有
,都有![]() ;
;
(2)函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(3)![]() ,對一切
,對一切![]() 恒成立;
恒成立;
(4)函數![]() 有
有![]() 個零點;
個零點;
(5)若關于![]() 的方程
的方程![]() 有且只有兩個不同的實根
有且只有兩個不同的實根![]() ,
,![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】箱子里有16張撲克牌:紅桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方塊
、6、5、4,方塊![]() 、5,老師從這16張牌中挑出一張牌來,并把這張牌的點數告訴了學生甲,把這張牌的花色告訴了學生乙,這時,老師問學生甲和學生乙:你們能從已知的點數或花色中推知這張牌是什么牌嗎?于是,老師聽到了如下的對話:學生甲:我不知道這張牌;學生乙:我知道你不知道這張牌;學生甲:現在我知道這張牌了;學生乙:我也知道了.則這張牌是( )
、5,老師從這16張牌中挑出一張牌來,并把這張牌的點數告訴了學生甲,把這張牌的花色告訴了學生乙,這時,老師問學生甲和學生乙:你們能從已知的點數或花色中推知這張牌是什么牌嗎?于是,老師聽到了如下的對話:學生甲:我不知道這張牌;學生乙:我知道你不知道這張牌;學生甲:現在我知道這張牌了;學生乙:我也知道了.則這張牌是( )
A. 草花5B. 紅桃![]()
C. 紅桃4D. 方塊5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“有黑掃黑、無黑除惡、無惡治亂”,維護社會穩定和和平發展.掃黑除惡期間,大量違法分子主動投案,某市公安機關對某月連續7天主動投案的人員進行了統計,![]() 表示第
表示第![]() 天主動投案的人數,得到統計表格如下:
天主動投案的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 與
與![]() 具有線性相關關系,請根據上表提供的數據,用最小二乘法求出
具有線性相關關系,請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)判定變量![]() 與
與![]() 之間是正相關還是負相關.(寫出正確答案,不用說明理由)
之間是正相關還是負相關.(寫出正確答案,不用說明理由)
(3)預測第八天的主動投案的人數(按四舍五入取到整數).
參考公式: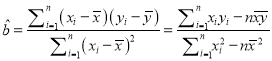 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農科院的專家為了了解新培育的甲、乙兩種麥苗的長勢情況,從種植有甲、乙兩種麥苗的兩塊試驗田中各抽取6株麥苗測量株高,得到的數據如下(單位:![]() ):
):
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21
(1)用莖葉圖表示這些數據:
(2)分別計算兩組數據的中位數、平均數與方差,并由此估計甲、乙兩種麥苗株高的平均數及方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列結論:
①若![]() 為真命題,則
為真命題,則![]() 、
、![]() 均為真命題;
均為真命題;
②命題“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() ”;
”;
③若命題![]() ,
,![]() ,則
,則![]() ,
,![]() ;
;
④“![]() ”是“
”是“![]() ”的充分不必要條件.其中正確的結論有____.
”的充分不必要條件.其中正確的結論有____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com