
 -x),求其定義域,并判斷其奇偶性、單調(diào)性.
-x),求其定義域,并判斷其奇偶性、單調(diào)性. -x>0,解得x∈R,即定義域為R.
-x>0,解得x∈R,即定義域為R.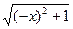 -(-x)]=lg(
-(-x)]=lg( +x)=lg
+x)=lg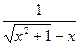 =lg(
=lg( -x)-1=-lg(
-x)-1=-lg( -x)=-f(x),∴y=lg(
-x)=-f(x),∴y=lg( -x)是奇函數(shù).任取x1、x2∈(0,+∞)且x1<x2,
-x)是奇函數(shù).任取x1、x2∈(0,+∞)且x1<x2,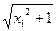 <
<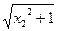
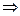
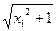 +x1<
+x1<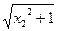 +x2
+x2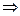
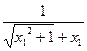 >
>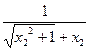 ,
,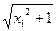 -x1>
-x1>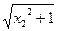 -x2>0,
-x2>0,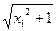 -x1)>lg(
-x1)>lg(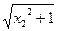 -x2),即f(x1)>f(x2)成立.
-x2),即f(x1)>f(x2)成立. +x=
+x=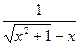 ,即有l(wèi)g(
,即有l(wèi)g( -x)=-lg(
-x)=-lg( +x),從而f(-x)=lg(
+x),從而f(-x)=lg( +x)=-lg(
+x)=-lg( -x)=-f(x),可知其為奇函數(shù).又因為奇函數(shù)在關(guān)于原點對稱的區(qū)間上的單調(diào)性相同,所以我們只需研究(0,+∞)上的單調(diào)性.
-x)=-f(x),可知其為奇函數(shù).又因為奇函數(shù)在關(guān)于原點對稱的區(qū)間上的單調(diào)性相同,所以我們只需研究(0,+∞)上的單調(diào)性.

科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.(0,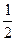 ) ) | B.(0,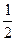 ] ] | C.(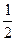 ,+∞) ,+∞) | D.(0,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.y=ex+1(x∈R) | B.y=ex-1(x∈R) |
| C.y=ex+1(x>1) | D.y=ex-1(x>1) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
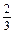 與log5
與log5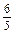 ;
;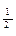 b<log
b<log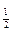 a<log
a<log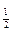 c,比較2b,2a,2c的大小關(guān)系.
c,比較2b,2a,2c的大小關(guān)系.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
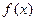 為定義在
為定義在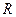 上的偶函數(shù),當(dāng)時,
上的偶函數(shù),當(dāng)時,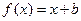 ,且
,且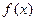 的圖象經(jīng)過點
的圖象經(jīng)過點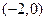 ,又在
,又在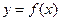 的圖象中,另一部分是頂點在(0,2),且過點(-1,1)的一段拋物線,試寫出函數(shù)
的圖象中,另一部分是頂點在(0,2),且過點(-1,1)的一段拋物線,試寫出函數(shù)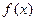 的表達式,并作出其圖象.
的表達式,并作出其圖象.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com