Question

12．對實數a和b，定義運算“⊕”：a⊕b=$\left\{\begin{array}{l}a，a-b≤1\\ b，a-b＞1\end{array}$．若函數f（x）=（x²-2）⊕（x-x²）-c，x∈R有兩個零點，則實數c的取值范圍為$（{-∞，-2}]∪（{-1，-\frac{3}{4}}）$．

Answer 1

分析 化簡函數f（x）的解析式，作出函數y=f（x）的圖象，由題意可得，函數y=f（x）與y=c的圖象有2個交點，結合圖象求得結果．

解答 解：當（x²-2）-（x-x²）≤1時，f（x）=x²-2，（-1≤x≤$\frac{3}{2}$），
當（x²-1）-（x-x²）＞1時，f（x）=x-x²，（x＞$\frac{3}{2}$或x＜-1），
函數y=f（x）的圖象如圖所示：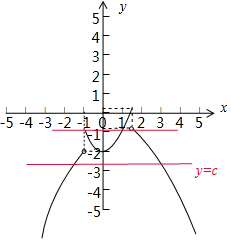

由圖象得：要使函數y=f（x）-c恰有2個零點，只要函數f（x）與y=c的圖形由2個交點即可，
所以：c∈$（{-∞，-2}]∪（{-1，-\frac{3}{4}}）$
故答案為：$（{-∞，-2}]∪（{-1，-\frac{3}{4}}）$．

點評 本題主要考查數形結合解決函數的零點個數問題，關鍵是正確畫圖、識圖；體現了化歸與轉化、數形結合的數學思想，屬于中檔題．