
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
分析 推導出A1C⊥BD,A1C⊥BC1,從而A1C⊥平面C1BD,以AA1為側棱補作一個正方體AEFG-A1PQS,使得側面AGRA1與平面ADD1A1共面,連結AQ,則AQ∥CA1,連結QB1,交A1R于S,則平面AQB1就是平面α,且AS為所求作,由此能求出結果.
解答 解:正方體ABCD-A1B1C1D1中,BD⊥AC,BD⊥AA1,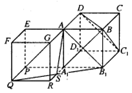
∵AC∩AA1=A,∴BD⊥平面AA1C,∴A1C⊥BD,
同理,得A1C⊥BC1,
∵BD∩BC1=B,∴A1C⊥平面C1BD,
如圖,以AA1為側棱補作一個正方體AEFG-A1PQS,
使得側面AGRA1與平面ADD1A1共面,
連結AQ,則AQ∥CA1,連結QB1,交A1R于S,則平面AQB1就是平面α,且AS為所求作,
∵AQ∥CA1,∴AQ⊥平面C1BD,
∵AQ?平面α,∴平面α⊥平面C1BD,
∴tan∠A1AS=$\frac{{A}_{1}S}{A{A}_{1}}$=$\frac{1}{2}$.
故選:D.
點評 本題考查平角的正切值的求法,考查空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力、數據處理能力,考查數形結合思想,是中檔題.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:選擇題
 函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f($\frac{π}{3}$)=( )
函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分圖象如圖所示,則f($\frac{π}{3}$)=( )| A. | $-\frac{1}{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
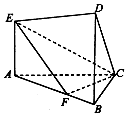 在如圖所示的幾何體中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如圖所示的幾何體中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | θ=$\frac{π}{12}$,t的最小值為$\frac{π}{12}$ | B. | θ=$\frac{π}{12}$,t的最小值為$\frac{π}{6}$ | ||
| C. | θ=$\frac{π}{6}$,t的最小值為$\frac{π}{6}$ | D. | θ=$\frac{π}{6}$,t的最小值為$\frac{π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com