
分析 (1)利用兩角差的三角公式化簡f(x)的解析式,再利用正弦函數的周期性和最值,求得f(x)的最小正周期和最大值.
(2)由條件利用同角三角函數的基本關系求得α的值,可得cos(α+β)=cos($\frac{π}{4}$+β)的值,從而求得tan(β+$\frac{π}{4}$)的值,再利用兩角差的三角公式求得tanβ=tan[($\frac{π}{4}$+β)-$\frac{π}{4}$]的值.
解答 解:(1)$f(x)=sin2xcos\frac{π}{4}-cos2xsin\frac{π}{4}+cos2xcos\frac{3π}{4}+sin2xsin\frac{3π}{4}$=$\sqrt{2}sin2x-\sqrt{2}cos2x=2sin(2x-\frac{π}{4})$,
故周期T=π,f(x)max=2.
(2)解:由$f(α)=\sqrt{2}$,得$sin(2α-\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,又$α∈(0,\frac{π}{2})$,所以$2α-\frac{π}{4}∈(-\frac{π}{4},\frac{3π}{4})$,∴$2α-\frac{π}{4}=\frac{π}{4}$,∴$α=\frac{π}{4}$.
∴$cos(α+β)=cos(\frac{π}{4}+β)=\frac{1}{3}$.
又$β∈(0,\frac{π}{2})$,∴$sin(\frac{π}{4}+β)=\sqrt{1-{{cos}^2}(\frac{π}{4}+β)}=\frac{{2\sqrt{2}}}{3}$,∴$tan(\frac{π}{4}+β)=\frac{{sin(\frac{π}{4}+β)}}{{cos(\frac{π}{4}+β)}}=2\sqrt{2}$,
∴$tanβ=tan(\frac{π}{4}+β-\frac{π}{4})=\frac{{tan(\frac{π}{4}+β)-tan\frac{π}{4}}}{{1+tan(\frac{π}{4}+β)tan\frac{π}{4}}}=\frac{{2\sqrt{2}-1}}{{1+2\sqrt{2}}}=\frac{{9-4\sqrt{2}}}{7}$.
點評 本題主要考查正弦函數的周期性和最值,同角三角函數的基本關系,兩角差的三角公式的應用,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\frac{\sqrt{3}}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{1}{3}$x |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
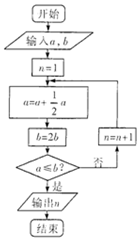 數學名著《算學啟蒙》中有如下問題:“松長五尺,竹長兩尺,松日自半,竹日自倍,松竹何日而長等.”如圖是源于其思想的一個程序框圖,若輸入的a,b的值分別為16,4,則輸出的n的值為( )
數學名著《算學啟蒙》中有如下問題:“松長五尺,竹長兩尺,松日自半,竹日自倍,松竹何日而長等.”如圖是源于其思想的一個程序框圖,若輸入的a,b的值分別為16,4,則輸出的n的值為( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | 7 | C. | 0 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com