
【題目】統計學中,經常用環比、同比來進行數據比較,環比是指本期統計數據與上期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比,同比是指本期數據與歷史同時期比較,如
月相比,同比是指本期數據與歷史同時期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比.
月相比.
環比增長率![]() (本期數
(本期數![]() 上期數)
上期數)![]() 上期數
上期數![]() ,
,
同比增長率![]() (本期數
(本期數![]() 同期數)
同期數)![]() 同期數
同期數![]() .
.
下表是某地區近![]() 個月來的消費者信心指數的統計數據:
個月來的消費者信心指數的統計數據:
序號 |
|
|
|
|
|
|
|
|
時間 |
|
|
|
|
|
|
|
|
消費者信心指數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求該地區
求該地區![]() 年
年![]() 月消費者信心指數的同比增長率(百分比形式下保留整數);
月消費者信心指數的同比增長率(百分比形式下保留整數);
![]() 除
除![]() 年
年![]() 月以外,該地區消費者信心指數月環比增長率為負數的有幾個月?
月以外,該地區消費者信心指數月環比增長率為負數的有幾個月?
![]() 由以上數據可判斷,序號
由以上數據可判斷,序號![]() 與該地區消費者信心指數
與該地區消費者信心指數![]() 具有線性相關關系,寫出
具有線性相關關系,寫出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小數),并依此預測該地區
位小數),并依此預測該地區![]() 年
年![]() 月的消費者信心指數(結果保留
月的消費者信心指數(結果保留![]() 位小數,參考數據與公式:
位小數,參考數據與公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
科目:高中數學 來源: 題型:
【題目】(選修4-4:坐標系與參數方程)
已知曲線C的極坐標方程是ρ=2cosθ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數方程是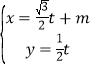 (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設點P(m,0),若直線L與曲線C交于A,B兩點,且|PA||PB|=1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某社區居民的業余生活狀況,研究這一社區居民在20:00-22:00時間段的休閑方式與性別的關系,隨機調查了該社區80人,得到下面的數據表:
休閑方式 性別 | 看電視 | 看書 | 合計 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合計 | 20 | 60 | 80 |
(1)根據以上數據,能否有![]() 的把握認為“在20:00-22:00時間段的休閑方式與性別有關系”?
的把握認為“在20:00-22:00時間段的休閑方式與性別有關系”?
(2)將此樣本的頻率估計為總體的概率,隨機調查3名在該社區的男性,設調查的3人在這一時間段以看書為休閑方式的人數為隨機變量![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
參考公式與數據![]() 對應
對應![]() ,
,![]() 對應
對應![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 。
。
Ⅰ.求函數![]() 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
Ⅱ.當![]() 時,方程
時,方程![]() 恰有兩個不同的實數根,求實數
恰有兩個不同的實數根,求實數![]() 的取值范圍;
的取值范圍;
Ⅲ.將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后所得函數
個單位后所得函數![]() 的圖象關于原點中心對稱,求
的圖象關于原點中心對稱,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】江蘇省園博會有一中心廣場,南京園,常州園都在中心廣場的南偏西45°方向上,到中心廣場的距離分別為![]() km,
km,![]() km;揚州園在中心廣場的正東方向,到中心廣場的距離為
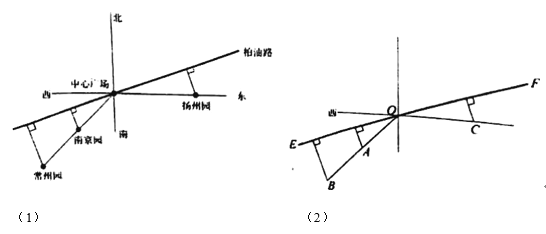
km;揚州園在中心廣場的正東方向,到中心廣場的距離為![]() km.規劃建設一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設成鵝卵石路(如圖(1)、(2)).已知鋪設每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數為2.設柏油路與正東方向的夾角,即圖(2)中∠COF為
km.規劃建設一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設成鵝卵石路(如圖(1)、(2)).已知鋪設每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數為2.設柏油路與正東方向的夾角,即圖(2)中∠COF為![]() (
(![]() (0,
(0,![]() )),鋪設三段鵝卵石路的總費用為y(萬元).
)),鋪設三段鵝卵石路的總費用為y(萬元).
(1)求南京園到柏油路的最短距離![]() 關于
關于![]() 的表達式;
的表達式;
(2)求y的最小值及此時tan![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的離心率是
的離心率是![]() ,過點
,過點![]() 的動直線
的動直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點,當直線
兩點,當直線![]() 平行
平行![]() 軸時,直線
軸時,直線![]() 被橢圓
被橢圓![]() 截得的線段長為4.
截得的線段長為4.

(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,是否存在常數
為坐標原點,是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com