
【題目】江蘇省園博會有一中心廣場,南京園,常州園都在中心廣場的南偏西45°方向上,到中心廣場的距離分別為![]() km,
km,![]() km;揚州園在中心廣場的正東方向,到中心廣場的距離為
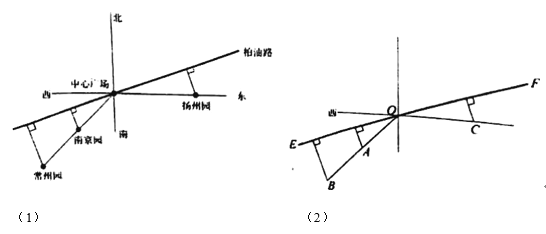
km;揚州園在中心廣場的正東方向,到中心廣場的距離為![]() km.規劃建設一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設成鵝卵石路(如圖(1)、(2)).已知鋪設每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數為2.設柏油路與正東方向的夾角,即圖(2)中∠COF為
km.規劃建設一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設成鵝卵石路(如圖(1)、(2)).已知鋪設每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數為2.設柏油路與正東方向的夾角,即圖(2)中∠COF為![]() (
(![]() (0,
(0,![]() )),鋪設三段鵝卵石路的總費用為y(萬元).
)),鋪設三段鵝卵石路的總費用為y(萬元).
(1)求南京園到柏油路的最短距離![]() 關于
關于![]() 的表達式;
的表達式;
(2)求y的最小值及此時tan![]() 的值.
的值.
【答案】(1)![]() ;(2)鋪設三條鵝卵石路的總費用為(
;(2)鋪設三條鵝卵石路的總費用為(![]() )萬元,此時
)萬元,此時![]() 的值為
的值為![]() .
.
【解析】
(1)由∠COF=θ,南京園在中心廣場的南偏西45°方向上,且到中心廣場的距離為![]() ,求出∠AOE=
,求出∠AOE=![]() ,由此能求出南京園到柏油路的最短距離d1關于θ的表達式.
,由此能求出南京園到柏油路的最短距離d1關于θ的表達式.
(2)分別設點B,C到直線EF的距離為d2,d3,則![]() ,求出y=2[(
,求出y=2[(![]() )2+(2
)2+(2![]() )2+(
)2+(![]() )2]=20﹣10
)2]=20﹣10![]() sin(2
sin(2![]() ),θ∈(0,
),θ∈(0,![]() ),由此能求出鋪設三條鵝卵石路的總費用y的最小值及此時tanθ的值.
),由此能求出鋪設三條鵝卵石路的總費用y的最小值及此時tanθ的值.
(1)∵∠COF=θ,
南京園在中心廣場的南偏西45°方向上,且到中心廣場的距離為![]()
∴∠AOE=![]() ,
,
∴南京園到柏油路的最短距離d1關于θ的表達式為d1=![]() sin(
sin(![]() ﹣θ).
﹣θ).
(2)分別設點B,C到直線EF的距離為d2,d3.
由(1)知:![]() ,
,
∴y=2[(![]() )2+(2
)2+(2![]() )2+(
)2+(![]() )2]
)2]
=20[![]() +
+![]() ]
]
=20﹣10(sin2θ+cos2θ)
=20﹣10![]() sin(2
sin(2![]() ),θ∈(0,
),θ∈(0,![]() ),
),
∵![]() ∴
∴![]() ,
,
∴當2![]() =
=![]() 時,ymin=20﹣10
時,ymin=20﹣10![]() (萬元)
(萬元)
此時2![]() ,
,
∴tan2θ=![]() =1,
=1,
解得:tan![]() ,
,
∴鋪設三條鵝卵石路的總費用為(20﹣10![]() )萬元,此時tanθ的值為
)萬元,此時tanθ的值為![]() .
.


科目:高中數學 來源: 題型:
【題目】有下列說法:
①在殘差圖中,殘差點比較均勻地落在水平的帶狀區域內,說明選用的模型比較合適;
②用相關指數R2來刻畫回歸的效果,R2值越大,說明模型的擬合效果越好;
③比較兩個模型的擬合效果,可以比較殘差平方和的大小,殘差平方和越小的模型,擬合效果越好.
④在研究氣溫和熱茶銷售杯數的關系時,若求得相關指數R2≈0.85,則表明氣溫解釋了15%的熱茶銷售杯數變化.
其中正確命題的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】統計學中,經常用環比、同比來進行數據比較,環比是指本期統計數據與上期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比,同比是指本期數據與歷史同時期比較,如
月相比,同比是指本期數據與歷史同時期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比.
月相比.
環比增長率![]() (本期數
(本期數![]() 上期數)
上期數)![]() 上期數
上期數![]() ,
,
同比增長率![]() (本期數
(本期數![]() 同期數)
同期數)![]() 同期數
同期數![]() .
.
下表是某地區近![]() 個月來的消費者信心指數的統計數據:
個月來的消費者信心指數的統計數據:
序號 |
|
|
|
|
|
|
|
|
時間 |
|
|
|
|
|
|
|
|
消費者信心指數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求該地區
求該地區![]() 年
年![]() 月消費者信心指數的同比增長率(百分比形式下保留整數);
月消費者信心指數的同比增長率(百分比形式下保留整數);
![]() 除
除![]() 年
年![]() 月以外,該地區消費者信心指數月環比增長率為負數的有幾個月?
月以外,該地區消費者信心指數月環比增長率為負數的有幾個月?
![]() 由以上數據可判斷,序號
由以上數據可判斷,序號![]() 與該地區消費者信心指數
與該地區消費者信心指數![]() 具有線性相關關系,寫出
具有線性相關關系,寫出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小數),并依此預測該地區
位小數),并依此預測該地區![]() 年
年![]() 月的消費者信心指數(結果保留
月的消費者信心指數(結果保留![]() 位小數,參考數據與公式:
位小數,參考數據與公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正方體![]() ,
,![]() 為棱
為棱![]() 的中點,
的中點,![]() 為棱
為棱![]() 的動點,設直線
的動點,設直線![]() 為平面
為平面![]() 與平面
與平面![]() 的交線,直線
的交線,直線![]() 為平面
為平面![]() 與平面
與平面![]() 的交線,下列結論中錯誤的是( )
的交線,下列結論中錯誤的是( )

A.![]() 平面
平面![]() B.平面
B.平面![]() 與平面
與平面![]() 不垂直
不垂直
C.平面![]() 與平面
與平面![]() 可能平行D.直線
可能平行D.直線![]() 與直線
與直線![]() 可能不平行
可能不平行
查看答案和解析>>
科目:高中數學 來源: 題型:
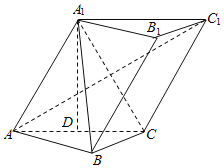
【題目】如圖,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.現以邊AC的中點D為坐標原點,平面ABC內垂直于AC的直線為![]() 軸,直線AC為
軸,直線AC為![]() 軸,直線DA1為
軸,直線DA1為![]() 軸建立空間直角坐標系,解決以下問題:
軸建立空間直角坐標系,解決以下問題:
(1)求異面直線AB與A1C所成角的余弦值;
(2)求直線AB與平面A1BC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱為可入肺顆粒物,一般情況下PM2.5的濃度越大,大氣環境質量越差.右邊的莖葉圖表示的是成都市區甲乙兩個監測站某10日內每天的PM2.5濃度讀數(單位:![]() ),則下列說法正確的是( )
),則下列說法正確的是( )

A.這10日內甲、乙監測站讀數的極差相等
B.這10日內甲、乙監測站讀數的中位數中,乙的較大
C.這10日內乙監測站讀數的眾數與中位數相等
D.這10日內甲、乙監測站讀數的平均數相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是半圓
是半圓![]() 的直徑,
的直徑,![]() ,
,![]() 為圓周上一點,
為圓周上一點,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,且使得
,且使得![]() 平面
平面![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com