
在平面直角坐標系上,設不等式組 所表示的平面區域為
所表示的平面區域為 ,記
,記 內的整點(即橫坐標和縱坐標均為整數的點)的個數為
內的整點(即橫坐標和縱坐標均為整數的點)的個數為 .
則
.
則 =
,經推理可得到
=
,經推理可得到 =
.
=
.
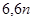
【解析】
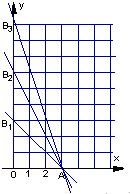
試題分析:根據題意,由x>0,y>0,-n(x-4)≥y>0得0<x≤4,
所以平面區域為Dn內的整點為點(4,0)與在直線x=1和x=2上,
∴直線y=-n(x-4)與直線x=1和x=2,x=3交點縱坐標分別為y1=3n和y2=2n, y3=n
∴Dn內在直線x=1和x=2上的整點個數分別為3n和2n,n
∴an=3n+2n+n=6n
當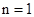 時,區域內的整點個數分別為6個,經推理可得到共
時,區域內的整點個數分別為6個,經推理可得到共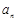 =
=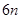 ,故答案為6,6n。
,故答案為6,6n。
考點:本題主要考查了平面區域內整點個數的問題的運用。
點評:解決該試題的關鍵是理解不等式對于x的限定范圍,然后分別對于x令值為1,2,3,得到整點的數,相加即為所求。


 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
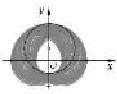 如圖,陰影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐標系上表示的點集,則陰影中間形如“水滴”部分的面積等于( )
如圖,陰影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐標系上表示的點集,則陰影中間形如“水滴”部分的面積等于( )A、π+
| ||||
B、
| ||||
C、
| ||||
| D、π+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 在平面直角坐標系上,設不等式組
在平面直角坐標系上,設不等式組
|
| 1 |
| Sn |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 1 |
| anan+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com