
【題目】已知拋物線![]() 的焦點曲線
的焦點曲線![]() 的一個焦點,
的一個焦點, ![]() 為坐標原點,點
為坐標原點,點![]() 為拋物線
為拋物線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸的平行線交拋物線的準線于
軸的平行線交拋物線的準線于![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)求證:直線![]() 過定點
過定點![]() ,并求出此定點的坐標.
,并求出此定點的坐標.
【答案】(I)![]() ;(II)證明見解析.
;(II)證明見解析.
【解析】試題分析:(Ⅰ)將曲線![]() 化為標準方程,可求得
化為標準方程,可求得![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,可得
,可得![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() ;(Ⅱ)結合(Ⅰ),可設
;(Ⅱ)結合(Ⅰ),可設![]() ,得
,得 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]() ,直線
,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() .
.
試題解析:(Ⅰ)由曲線![]() ,化為標準方程可得
,化為標準方程可得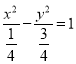 , 所以曲線
, 所以曲線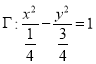 是焦點在
是焦點在![]() 軸上的雙曲線,其中
軸上的雙曲線,其中![]() ,故
,故![]() ,
, ![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,因為拋物線的焦點坐標為
,因為拋物線的焦點坐標為![]() ,由題意知
,由題意知![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() .
.
(Ⅱ)由(Ⅰ)知拋物線![]() 的準線方程為
的準線方程為![]() ,設
,設![]() ,顯然
,顯然![]() .故
.故 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]()
①當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,
,
②當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() ,
, ![]() 也在直線
也在直線![]() 的方程為
的方程為![]() 上,故直線
上,故直線![]() 的方程恒過定點
的方程恒過定點![]() .
.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,
, ![]()
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)若![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)證明見解析.
;(III)證明見解析.
【解析】試題分析:(Ⅰ)求出![]() ,在定義域內,分別令
,在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(Ⅱ)當
的減區間;(Ⅱ)當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,先證明因此
顯然不成立,先證明因此![]() 時,
時, ![]() 在
在![]() 上恒成立,再證明當
上恒成立,再證明當![]() 時不滿足題意,從而可得結果;(III)先求出等差數列的前
時不滿足題意,從而可得結果;(III)先求出等差數列的前![]() 項和為
項和為![]() ,結合(II)可得
,結合(II)可得![]() ,各式相加即可得結論.
,各式相加即可得結論.
試題解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函數
(舍去),所以函數![]() 的單調遞減區間為
的單調遞減區間為 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,因此
顯然不成立,因此![]() .
.
令![]() ,則
,則 ,令
,令![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 時,
時, ![]() 在
在![]() 上恒成立.
上恒成立.
②當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數,
上為增函數,
∴![]() ,不滿足題意.
,不滿足題意.
綜上,不等式![]() 在
在![]() 上恒成立時,實數
上恒成立時,實數![]() 的取值范圍是
的取值范圍是![]() .
.
(III)證明:由![]() 知數列
知數列![]() 是
是![]() 的等差數列,所以
的等差數列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 將以上各式左右兩邊分別相加,得
. 將以上各式左右兩邊分別相加,得
![]() .因為
.因為![]()
所以![]()
所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】我們稱一個非負整數集合![]() (非空)為好集合,若對任意
(非空)為好集合,若對任意![]() ,或者
,或者![]() ,或者
,或者![]() .以下記
.以下記![]() 為
為![]() 的元素個數.
的元素個數.
(Ⅰ)給出所有的元素均小于![]() 的好集合;(給出結論即可)
的好集合;(給出結論即可)
(Ⅱ)求出所有滿足![]() 的好集合;(同時說明理由)
的好集合;(同時說明理由)
(Ⅲ)若好集合![]() 滿足
滿足![]() ,求證:
,求證: ![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均為
中所有元素均為![]() 的整數倍.
的整數倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() 與常數
與常數![]() ,若
,若![]() 恒成立,則稱
恒成立,則稱![]() 為函數
為函數![]() 的一個“
的一個“![]() 數對”;設函數
數對”;設函數![]() 的定義域為
的定義域為![]() ,且
,且![]() .
.
(Ⅰ)若![]() 是
是![]() 的一個“
的一個“![]() 數對”,且
數對”,且![]() ,求常數
,求常數![]() 的值;
的值;
(Ⅱ)若![]() 是
是![]() 的一個“
的一個“![]() 數對”,求
數對”,求![]() ;
;
(Ⅲ)若![]() 是
是![]() 的一個“
的一個“![]() 數對”,且當
數對”,且當![]() ,
, ![]() ,求
,求![]() 的值及
的值及![]() 在區間
在區間![]() 上的最大值與最小值.
上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的圖象與
)的圖象與![]() 軸的交點中,相鄰兩個交點之間的距離為
軸的交點中,相鄰兩個交點之間的距離為![]() ,且圖象上一個最高點為
,且圖象上一個最高點為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)先把函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數
個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數![]() 的圖象,試寫出函數
的圖象,試寫出函數![]() 的解析式.
的解析式.
(3)在(2)的條件下,若存在![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是半圓
是半圓![]() 的直徑,
的直徑,![]() ,
,![]() 是將半圓圓周四等分的三個分點.
是將半圓圓周四等分的三個分點.

(1)從![]() 這5個點中任取3個點,求這3個點組成直角三角形的概率;
這5個點中任取3個點,求這3個點組成直角三角形的概率;
(2)在半圓內任取一點![]() ,求
,求![]() 的面積大于
的面積大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年初,湖北出現由新型冠狀病毒引發的肺炎.各級政府相繼啟動重大突發公共衛生事件一級響應,全國齊心抗擊疫情,基本上控制住了疫情.下圖為
年初,湖北出現由新型冠狀病毒引發的肺炎.各級政府相繼啟動重大突發公共衛生事件一級響應,全國齊心抗擊疫情,基本上控制住了疫情.下圖為![]() 月
月![]() 日至
日至![]() 月
月![]() 日我國新型冠狀病毒肺炎全國總新增確診人數和新增境外輸入確診人數趨勢圖(數據來源:國家衛健委官網),則下列表述中錯誤的是( )
日我國新型冠狀病毒肺炎全國總新增確診人數和新增境外輸入確診人數趨勢圖(數據來源:國家衛健委官網),則下列表述中錯誤的是( )

A.3月上旬全國總新增確診人數呈波動下降趨勢.
B.3月中下旬全國總新增確診人數開始反彈的主要原因是境外輸入病例的增加.
C.全國總新增確診人數隨著境外輸入確診人數變化而變化.
D.4月中下旬國內新增確診人數呈越來越少的趨勢.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com