
【題目】我們稱一個非負整數集合![]() (非空)為好集合,若對任意
(非空)為好集合,若對任意![]() ,或者
,或者![]() ,或者
,或者![]() .以下記
.以下記![]() 為
為![]() 的元素個數.
的元素個數.
(Ⅰ)給出所有的元素均小于![]() 的好集合;(給出結論即可)
的好集合;(給出結論即可)
(Ⅱ)求出所有滿足![]() 的好集合;(同時說明理由)
的好集合;(同時說明理由)
(Ⅲ)若好集合![]() 滿足
滿足![]() ,求證:
,求證: ![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均為
中所有元素均為![]() 的整數倍.
的整數倍.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,過
,過![]() 任作一條與坐標軸都不垂直的直線,與
任作一條與坐標軸都不垂直的直線,與![]() 交于
交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .當直線
.當直線![]() 的斜率為
的斜率為![]() 時,
時,![]() 與
與![]() 軸垂直
軸垂直
(1)求橢圓![]() 的方程
的方程
(2)若![]() 是該橢圓上位于第一象限的一點,過
是該橢圓上位于第一象限的一點,過![]() 作圓
作圓![]() 的切線,切點為
的切線,切點為![]() ,求
,求![]() 的值;
的值;
(3)設![]() 為定點,直線
為定點,直線![]() 過點
過點![]() 與
與![]() 軸交于點
軸交于點![]() ,且與橢圓交于
,且與橢圓交于![]() 兩點,設
兩點,設![]() ,
,![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖中實線所示,圖中圓C與
)的部分圖象如圖中實線所示,圖中圓C與![]() 的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )
的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )

A.函數![]() 的最小正周期是2π
的最小正周期是2π
B.函數![]() 的圖象關于點
的圖象關于點![]() 成中心對稱
成中心對稱
C.函數![]() 在
在![]() 單調遞增
單調遞增
D.將函數![]() 的圖象向左平移
的圖象向左平移![]() 后得到的關于y軸對稱
后得到的關于y軸對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新冠肺炎疫情期間,為了減少外出聚集,“線上買菜”受追捧.某電商平臺在![]() 地區隨機抽取了
地區隨機抽取了![]() 位居民進行調研,獲得了他們每個人近七天“線上買菜”消費總金額(單位:元),整理得到如圖所示頻率分布直方圖.
位居民進行調研,獲得了他們每個人近七天“線上買菜”消費總金額(單位:元),整理得到如圖所示頻率分布直方圖.

(1)求![]() 的值;
的值;
(2)從“線上買菜”消費總金額不低于![]() 元的被調研居民中,隨機抽取
元的被調研居民中,隨機抽取![]() 位給予獎品,求這
位給予獎品,求這![]() 位“線上買菜”消費總金額均低于
位“線上買菜”消費總金額均低于![]() 元的概率;
元的概率;
(3)若![]() 地區有
地區有![]() 萬居民,該平臺為了促進消費,擬對消費總金額不到平均水平一半的居民投放每人
萬居民,該平臺為了促進消費,擬對消費總金額不到平均水平一半的居民投放每人![]() 元的電子補貼.假設每組中的數據用該組區間的中點值代替,試根據上述頻率分布直方圖,估計該平臺在
元的電子補貼.假設每組中的數據用該組區間的中點值代替,試根據上述頻率分布直方圖,估計該平臺在![]() 地區擬投放的電子補貼總金額.
地區擬投放的電子補貼總金額.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某單位45名職工中隨機抽取5名職工參加一項社區服務活動,用隨機數法確定這5名職工![]() 現將隨機數表摘錄部分如下:
現將隨機數表摘錄部分如下:
![]()
![]()
從隨機數表第一行的第5列和第6列數字開始由左到右依次選取兩個數字,則選出的第5個職工的編號為![]()
A.23B.37C.35D.17
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 是函數
是函數![]() 的圖象的一個對稱中心,且點
的圖象的一個對稱中心,且點![]() 到該圖象的對稱軸的距離的最小值為
到該圖象的對稱軸的距離的最小值為![]() .
.
①![]() 的最小正周期是
的最小正周期是![]() ;
;
②![]() 的值域為
的值域為![]() ;
;
③![]() 的初相
的初相![]() 為
為![]() ;
;
④![]() 在
在![]() 上單調遞增.
上單調遞增.
以上說法正確的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,圓
,圓![]() ,點
,點![]() 是圓上一動點,線段
是圓上一動點,線段![]() 的中垂線與線段
的中垂線與線段![]() 交于點
交于點![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,且存在點
兩點,且存在點![]() (其中
(其中![]() 不共線),使得
不共線),使得![]() 被
被![]() 軸平分,證明:直線
軸平分,證明:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三角形內,我們將三條邊的中線的交點稱為三角形的重心,且重心到任一頂點的距離是到對邊中點距離的兩倍類比上述結論:在三棱錐中,我們將頂點與對面重心的連線段稱為三棱錐的“中線”,將三棱錐四條中線的交點稱為它的“重心”,則棱錐重心到頂點的距離是到對面重心距離的______倍![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點曲線
的焦點曲線![]() 的一個焦點,
的一個焦點, ![]() 為坐標原點,點
為坐標原點,點![]() 為拋物線
為拋物線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 軸的平行線交拋物線的準線于
軸的平行線交拋物線的準線于![]() ,直線
,直線![]() 交拋物線于點
交拋物線于點![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)求證:直線![]() 過定點
過定點![]() ,并求出此定點的坐標.
,并求出此定點的坐標.
【答案】(I)![]() ;(II)證明見解析.
;(II)證明見解析.
【解析】試題分析:(Ⅰ)將曲線![]() 化為標準方程,可求得
化為標準方程,可求得![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,可得
,可得![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() ;(Ⅱ)結合(Ⅰ),可設
;(Ⅱ)結合(Ⅰ),可設![]() ,得
,得 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]() ,直線
,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() .
.
試題解析:(Ⅰ)由曲線![]() ,化為標準方程可得
,化為標準方程可得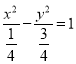 , 所以曲線
, 所以曲線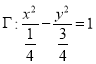 是焦點在
是焦點在![]() 軸上的雙曲線,其中
軸上的雙曲線,其中![]() ,故
,故![]() ,
, ![]() 的焦點坐標分別為
的焦點坐標分別為![]() ,因為拋物線的焦點坐標為
,因為拋物線的焦點坐標為![]() ,由題意知
,由題意知![]() ,所以
,所以![]() ,即拋物線的方程為
,即拋物線的方程為![]() .
.
(Ⅱ)由(Ⅰ)知拋物線![]() 的準線方程為
的準線方程為![]() ,設
,設![]() ,顯然
,顯然![]() .故
.故 ,從而直線
,從而直線![]() 的方程為
的方程為![]() ,聯立直線與拋物線方程得
,聯立直線與拋物線方程得![]() ,解得
,解得![]()
①當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,
,
②當![]() ,即
,即![]() 時,直線
時,直線![]() 的方程為
的方程為 ,整理得
,整理得![]() 的方程為
的方程為![]() ,此時直線恒過定點
,此時直線恒過定點![]() ,
, ![]() 也在直線
也在直線![]() 的方程為
的方程為![]() 上,故直線
上,故直線![]() 的方程恒過定點
的方程恒過定點![]() .
.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,
, ![]()
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)若![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com