
【題目】點![]() 是函數
是函數![]() 的圖象的一個對稱中心,且點
的圖象的一個對稱中心,且點![]() 到該圖象的對稱軸的距離的最小值為
到該圖象的對稱軸的距離的最小值為![]() .
.
①![]() 的最小正周期是
的最小正周期是![]() ;
;
②![]() 的值域為
的值域為![]() ;
;
③![]() 的初相
的初相![]() 為
為![]() ;
;
④![]() 在
在![]() 上單調遞增.
上單調遞增.
以上說法正確的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由條件利用正弦函數的周期性、單調性、最值,以及圖象的對稱性,即可得出結論.
∵點P(﹣![]() ,1)是函數f(x)=sin(ωx+φ)+m(ω>0,|φ|<
,1)是函數f(x)=sin(ωx+φ)+m(ω>0,|φ|<![]() )的圖象的一個對稱中心,∴m=1,ω(﹣
)的圖象的一個對稱中心,∴m=1,ω(﹣![]() )+φ=kπ,k∈Z.
)+φ=kπ,k∈Z.
∵點P到該圖象的對稱軸的距離的最小值為![]() ,∴ω=2,
,∴ω=2,
∴φ=kπ+![]() , k∈Z,又|φ|<
, k∈Z,又|φ|<![]() ∴φ=
∴φ=![]() ,f(x)=sin(2x+
,f(x)=sin(2x+![]() )+1.
)+1.
故①f(x)的最小正周期是π,正確;②f(x)的值域為[0,2],正確;
③f(x)的初相φ為![]() ,正確;
,正確;
④在[![]() ,2π]上,2x+
,2π]上,2x+![]() ∈[
∈[![]() ,
,![]() ],根據函數的周期性,函數單調性與 [﹣
],根據函數的周期性,函數單調性與 [﹣![]() ,
,![]() ]時的單調性相同,故函數f(x)單調遞增,故④正確,
]時的單調性相同,故函數f(x)單調遞增,故④正確,
故選:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】表示一位騎自行車和一位騎摩托車的旅行者在相距80 km的甲、乙兩城間從甲城到乙城所行駛的路程與時間之間的函數關系,有人根據函數圖象,提出了關于這兩個旅行者的如下信息:

①騎自行車者比騎摩托車者早出發3 h,晚到1 h;
②騎自行車者是變速運動,騎摩托車者是勻速運動;
③騎摩托車者在出發1.5 h后追上了騎自行車者;
④騎摩托車者在出發1.5 h后與騎自行車者速度一樣.
其中,正確信息的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直角![]() 的三邊長
的三邊長![]() ,滿足
,滿足![]() .
.
(Ⅰ)在![]() 之間插入
之間插入![]() 個數,使這
個數,使這![]() 個數構成以
個數構成以![]() 為首項的等差數列
為首項的等差數列![]() ,且它們的和為
,且它們的和為![]() ,求斜邊的最小值;
,求斜邊的最小值;
(Ⅱ)已知![]() 均為正整數,且
均為正整數,且![]() 成等差數列,將滿足條件的三角形的面積從小到大排成一列
成等差數列,將滿足條件的三角形的面積從小到大排成一列![]() ,且
,且![]() ,求滿足不等式
,求滿足不等式![]() 的所有
的所有![]() 的值;
的值;
(Ⅲ)已知![]() 成等比數列,若數列
成等比數列,若數列![]() 滿足
滿足![]() ,證明:數列
,證明:數列![]() 中的任意連續三項為邊長均可以構成直角三角形,且
中的任意連續三項為邊長均可以構成直角三角形,且![]() 是正整數.
是正整數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們稱一個非負整數集合![]() (非空)為好集合,若對任意
(非空)為好集合,若對任意![]() ,或者
,或者![]() ,或者
,或者![]() .以下記
.以下記![]() 為
為![]() 的元素個數.
的元素個數.
(Ⅰ)給出所有的元素均小于![]() 的好集合;(給出結論即可)
的好集合;(給出結論即可)
(Ⅱ)求出所有滿足![]() 的好集合;(同時說明理由)
的好集合;(同時說明理由)
(Ⅲ)若好集合![]() 滿足
滿足![]() ,求證:
,求證: ![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均為
中所有元素均為![]() 的整數倍.
的整數倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某銀行對某市最近5年住房貸款發放情況(按每年6月份與前一年6月份為1年統計)作了統計調查,得到如下數據:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
貸款 | 50 | 60 | 70 | 80 | 100 |
(1)將上表進行如下處理:![]() ,
,
得到數據:
| 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
試求![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,再寫出
,再寫出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)利用(1)中所求的線性回歸方程估算2019年房貸發放數額.
參考公式: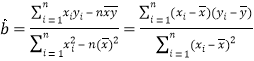 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為![]() ,其中
,其中![]() 為參數,且
為參數,且![]() 在直角坐標系
在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 是曲線
是曲線![]() 上的一點,直線
上的一點,直線![]() 被曲線
被曲線![]() 截得的弦長為
截得的弦長為![]() ,求
,求![]() 點的極坐標.
點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的圖象與
)的圖象與![]() 軸的交點中,相鄰兩個交點之間的距離為
軸的交點中,相鄰兩個交點之間的距離為![]() ,且圖象上一個最高點為
,且圖象上一個最高點為![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)先把函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數
個單位長度,然后再把所得圖象上各點的橫坐標伸長到原來的2倍(縱坐標不變),得到函數![]() 的圖象,試寫出函數
的圖象,試寫出函數![]() 的解析式.
的解析式.
(3)在(2)的條件下,若存在![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com