
【題目】已知直角![]() 的三邊長
的三邊長![]() ,滿足
,滿足![]() .
.
(Ⅰ)在![]() 之間插入
之間插入![]() 個數,使這
個數,使這![]() 個數構成以
個數構成以![]() 為首項的等差數列
為首項的等差數列![]() ,且它們的和為
,且它們的和為![]() ,求斜邊的最小值;
,求斜邊的最小值;
(Ⅱ)已知![]() 均為正整數,且
均為正整數,且![]() 成等差數列,將滿足條件的三角形的面積從小到大排成一列
成等差數列,將滿足條件的三角形的面積從小到大排成一列![]() ,且
,且![]() ,求滿足不等式
,求滿足不等式![]() 的所有
的所有![]() 的值;
的值;
(Ⅲ)已知![]() 成等比數列,若數列
成等比數列,若數列![]() 滿足
滿足![]() ,證明:數列
,證明:數列![]() 中的任意連續三項為邊長均可以構成直角三角形,且
中的任意連續三項為邊長均可以構成直角三角形,且![]() 是正整數.
是正整數.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
解:(Ⅰ)![]() 是等差數列,
是等差數列, ![]() ,即
,即![]() .
.
![]() ,斜邊的最小值為
,斜邊的最小值為![]() (當且僅當
(當且僅當![]() 等號成立,
等號成立,
此時數列![]() 中,
中, ![]() .
.
(Ⅱ)設![]() 的公差為
的公差為![]() ,則
,則![]() ,
,![]() .
.
設三角形的三邊長為![]() 面積
面積![]() ,
,
![]() ,
,
![]()
由![]() 得
得![]() .
.
當![]() 時,
時, ![]() ,
,
經檢驗當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
綜上所述,滿足不等式![]() 的所有
的所有![]() 的值為
的值為![]() .
.
(Ⅲ)證明:因為![]() 成等比數列,
成等比數列, ![]() ,
,
因為![]() 為直角三角形的三邊長,知
為直角三角形的三邊長,知![]() ,
,
又![]() ,得
,得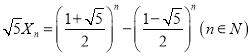 ,
,
于是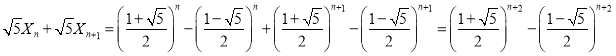 ,
,
![]() ,
,
則有![]() ,
,
故數列![]() 中的任意連續三項為邊長均可以構成直角三角形.
中的任意連續三項為邊長均可以構成直角三角形.
因為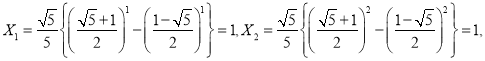
![]() ,
,
由![]() ,同理可得
,同理可得![]() ,
,
故對于任意的![]() 都有
都有![]() 是正整數.
是正整數.
【解析】試題分析:(Ⅰ) ![]() 是等差數列,
是等差數列, ![]() ,即
,即![]() ..
..
利用勾股定理與基本不等式的性質即可得出.
(Ⅱ)設![]() 的公差為
的公差為![]() ,則
,則![]() ,
,![]() .
.
設三角形的三邊長為![]() 面積
面積![]() ,
,
![]() ,利用等差數列的求和公式可得
,利用等差數列的求和公式可得![]() .由
.由![]() 得
得![]() ,經過分類討論即可得出.
,經過分類討論即可得出.
(Ⅲ)由![]() 成等比數列,
成等比數列, ![]() ,因為
,因為![]() 為直角三角形的三邊長,
為直角三角形的三邊長,
知![]() ,
,
又 ,,可得
,,可得![]() ,再利用勾股定理進行驗證即可得出.
,再利用勾股定理進行驗證即可得出.
試題解析:
(Ⅰ)![]() 是等差數列,
是等差數列, ![]() ,即
,即![]() .
.
![]() ,斜邊的最小值為
,斜邊的最小值為![]() (當且僅當
(當且僅當![]() 等號成立,
等號成立,
此時數列![]() 中,
中, ![]() .
.
(Ⅱ)設![]() 的公差為
的公差為![]() ,則
,則![]() ,
,![]() .
.
設三角形的三邊長為![]() 面積
面積![]() ,
,
![]() ,
,
![]()
由![]() 得
得![]() .
.
當![]() 時,
時, ![]() ,
,
經檢驗當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
綜上所述,滿足不等式![]() 的所有
的所有![]() 的值為
的值為![]() .
.
(Ⅲ)證明:因為![]() 成等比數列,
成等比數列, ![]() ,
,
因為![]() 為直角三角形的三邊長,知
為直角三角形的三邊長,知![]() ,
,
又![]() ,得
,得 ,
,
于是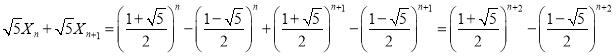 ,
,
![]() ,
,
則有![]() ,
,
故數列![]() 中的任意連續三項為邊長均可以構成直角三角形.
中的任意連續三項為邊長均可以構成直角三角形.
因為
![]() ,
,
由![]() ,同理可得
,同理可得![]() ,
,
故對于任意的![]() 都有
都有![]() 是正整數.
是正整數.


科目:高中數學 來源: 題型:
【題目】某同學在生物研究性學習中,對春季晝夜溫差大小與黃豆種子發芽多少之間的關系進行研究,于是他在4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每100顆種子浸泡后的發芽數,得到如下資料:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發芽數 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,求這2天發芽的種子數均不小于25的概率;
(2)從這5天中任選2天,若選取的是4月1日與4月30日的兩組數據,請根據這5天中的另三天的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得的線性回歸方程是否可靠?
附:回歸直線的斜率和截距的最小二乘估計公式分別為 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三國時期著名的數學家劉徽對推導特殊數列的求和公式很感興趣,創造并發展了許多算法,展現了聰明才智.他在《九章算術》“盈不足”章的第19題的注文中給出了一個特殊數列的求和公式.這個題的大意是:一匹良馬和一匹駑馬由長安出發至齊地,長安與齊地相距3000里(1里=500米),良馬第一天走193里,以后每天比前一天多走13里.駑馬第一天走97里,以后每天比前一天少走半里.良馬先到齊地后,馬上返回長安迎駑馬,問兩匹馬在第幾天相遇( )
A. 14天B. 15天C. 16天D. 17天
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖中實線所示,圖中圓C與
)的部分圖象如圖中實線所示,圖中圓C與![]() 的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )
的圖象交于M,N兩點,且M在y軸上,則下列說法中正確的是( )

A.函數![]() 的最小正周期是2π
的最小正周期是2π
B.函數![]() 的圖象關于點
的圖象關于點![]() 成中心對稱
成中心對稱
C.函數![]() 在
在![]() 單調遞增
單調遞增
D.將函數![]() 的圖象向左平移
的圖象向左平移![]() 后得到的關于y軸對稱
后得到的關于y軸對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的菱形,側面
的菱形,側面![]() 底面
底面![]() ,
,![]() 60°,
60°, ![]() ,
, ![]() 是
是![]() 中點,點
中點,點![]() 在側棱
在側棱![]() 上.
上.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)是否存在![]() ,使平面
,使平面![]()
![]() 平面
平面![]() ?若存在,求出,若不存在,說明理由.
?若存在,求出,若不存在,說明理由.
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出.若不存在,說明理由.
?若存在,求出.若不存在,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新冠肺炎疫情期間,為了減少外出聚集,“線上買菜”受追捧.某電商平臺在![]() 地區隨機抽取了
地區隨機抽取了![]() 位居民進行調研,獲得了他們每個人近七天“線上買菜”消費總金額(單位:元),整理得到如圖所示頻率分布直方圖.
位居民進行調研,獲得了他們每個人近七天“線上買菜”消費總金額(單位:元),整理得到如圖所示頻率分布直方圖.

(1)求![]() 的值;
的值;
(2)從“線上買菜”消費總金額不低于![]() 元的被調研居民中,隨機抽取
元的被調研居民中,隨機抽取![]() 位給予獎品,求這
位給予獎品,求這![]() 位“線上買菜”消費總金額均低于
位“線上買菜”消費總金額均低于![]() 元的概率;
元的概率;
(3)若![]() 地區有
地區有![]() 萬居民,該平臺為了促進消費,擬對消費總金額不到平均水平一半的居民投放每人
萬居民,該平臺為了促進消費,擬對消費總金額不到平均水平一半的居民投放每人![]() 元的電子補貼.假設每組中的數據用該組區間的中點值代替,試根據上述頻率分布直方圖,估計該平臺在
元的電子補貼.假設每組中的數據用該組區間的中點值代替,試根據上述頻率分布直方圖,估計該平臺在![]() 地區擬投放的電子補貼總金額.
地區擬投放的電子補貼總金額.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】點![]() 是函數
是函數![]() 的圖象的一個對稱中心,且點
的圖象的一個對稱中心,且點![]() 到該圖象的對稱軸的距離的最小值為
到該圖象的對稱軸的距離的最小值為![]() .
.
①![]() 的最小正周期是
的最小正周期是![]() ;
;
②![]() 的值域為
的值域為![]() ;
;
③![]() 的初相
的初相![]() 為
為![]() ;
;
④![]() 在
在![]() 上單調遞增.
上單調遞增.
以上說法正確的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據下列條件解三角形,有兩解的有( )
A.已知a![]() ,b=2,B=45°B.已知a=2,b
,b=2,B=45°B.已知a=2,b![]() ,A=45°
,A=45°
C.已知b=3,c![]() ,C=60°D.已知a=2
,C=60°D.已知a=2![]() ,c=4,A=45°
,c=4,A=45°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com