【題目】若長方體
的底面是邊長為2的正方形，高為4，
是
的中點，則（ ）
A.
B.平面
平面
C.三棱錐
的體積為
D.三棱錐
的外接球的表面積為
【答案】CD
【解析】
以
為正交基底建立空間直角坐標系，寫出各點坐標，計算
值即可判斷A；分別求出平面
，平面
的法向量，判斷它們的法向量是否共線，即可判斷B；利用等體積法，求出三棱錐
的體積即可判斷C；三棱錐
的外接球即為長方體
的外接球，故求出長方體的外接球的表面積即可判斷D.
以為正交基底建立如圖所示的空間直角坐標系，則
，
，
，
，
，
，
，
所以
，
，
因為
，所以
與
不垂直，故A錯誤；
，
設平面的一個法向量為
，則
由
，得
，所以
，
不妨取
，則
，
所以
，
同理可得設平面的一個法向量為
，
故不存在實數
使得
，故平面與平面不平行，故B錯誤；
在長方體中，
平面
，
故
是三棱錐
的高，
所以
，
故C正確；
三棱錐的外接球即為長方體的外接球，
故外接球的半徑
，
所以三棱錐的外接球的表面積
，故D正確.
故選：CD.
開心蛙狀元測試卷系列答案科目：高中數學 來源： 題型：
【題目】從某單位45名職工中隨機抽取5名職工參加一項社區服務活動，用隨機數法確定這5名職工
現將隨機數表摘錄部分如下：
從隨機數表第一行的第5列和第6列數字開始由左到右依次選取兩個數字，則選出的第5個職工的編號為
A.23B.37C.35D.17
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點曲線
的一個焦點， 
為坐標原點，點
為拋物線
上任意一點，過點
作
軸的平行線交拋物線的準線于
，直線
交拋物線于點
.
（Ⅰ）求拋物線
的方程；
（Ⅱ）求證：直線
過定點
，并求出此定點的坐標.
【答案】（I）
；（II）證明見解析.
【解析】試題分析：（Ⅰ）將曲線
化為標準方程，可求得
的焦點坐標分別為
，可得
，所以
，即拋物線的方程為
；（Ⅱ）結合（Ⅰ），可設
，得
，從而直線
的方程為
,聯立直線與拋物線方程得
，解得
，直線
的方程為
，整理得
的方程為
，此時直線恒過定點
.
試題解析：（Ⅰ）由曲線
，化為標準方程可得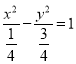
， 所以曲線
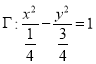是焦點在
軸上的雙曲線，其中
，故
， 
的焦點坐標分別為
，因為拋物線的焦點坐標為
，由題意知
，所以
，即拋物線的方程為
.
（Ⅱ）由（Ⅰ）知拋物線
的準線方程為
，設
，顯然
.故
，從而直線
的方程為
,聯立直線與拋物線方程得
，解得
①當
，即
時，直線
的方程為
，
②當
，即
時，直線
的方程為
，整理得
的方程為
，此時直線恒過定點
， 
也在直線
的方程為
上，故直線
的方程恒過定點
.
【題型】解答題
【結束】
21
【題目】已知函數
， 
（Ⅰ）當
時，求函數
的單調遞減區間；
（Ⅱ）若
時，關于
的不等式
恒成立，求實數
的取值范圍；
（Ⅲ）若數列
滿足
， 
，記
的前
項和為
，求證： 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】祖暅是我國南北朝時期杰出的數學家和天文學家祖沖之的兒子，他提出了一條原理：“冪勢既同冪，則積不容異”.這里的“冪”指水平截面的面積，“勢”指高.這句話的意思是：兩個等高的幾何體若在所有等高處的水平截面的面積相等，則這兩個幾何體體積相等.一般大型熱電廠的冷卻塔大都采用雙曲線型.設某雙曲線型冷卻塔是曲線
與直線
， 
和
所圍成的平面圖形繞
軸旋轉一周所得，如圖所示.試應用祖暅原理類比求球體體積公式的方法，求出此冷卻塔的體積為_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】總體由編號為01，02，…，19，20的20個個體組成，利用下面的隨機數表選取6個個體，選取方法從隨機數表第1行的第5列和第6列數字開始由左到右依次選取兩個數字，則選出來的第6個個體的編號為（ ）
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A.07B.04C.02D.01
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
