
【題目】已知a,b,c分別為![]() 內角A,B,C的對邊,若
內角A,B,C的對邊,若![]() 同時滿足以下四個條件中的三個:①
同時滿足以下四個條件中的三個:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)條件①②能否同時滿足,請說明理由;
(2)以上四個條件,請在滿足三角形有解的所有組合中任選一組,并求出對應![]() 的面積.
的面積.
【答案】(1)不能同時滿足①② (2)若![]() 滿足①③④時,則
滿足①③④時,則![]() 的面積為
的面積為![]() ,若
,若![]() 滿足②③④時,則
滿足②③④時,則![]() 的面積為
的面積為![]() .
.
【解析】
(1)由①根據余弦定理得到![]() ,進一步得到
,進一步得到![]() ,由②結合正弦定理得到
,由②結合正弦定理得到![]() ,從而得到
,從而得到![]() 不成立,由此可得答案;
不成立,由此可得答案;
(2)由(1)知,![]() 滿足①③④或②③④,若
滿足①③④或②③④,若![]() 滿足①③④,根據余弦定理求出
滿足①③④,根據余弦定理求出![]() ,再根據三角形的面積公式可得面積;若
,再根據三角形的面積公式可得面積;若![]() 滿足②③④,根據正弦定理得到
滿足②③④,根據正弦定理得到![]() ,由勾股定理求出
,由勾股定理求出![]() ,根據直角三角形的面積公式可得面積.
,根據直角三角形的面積公式可得面積.
(1)由①![]() 得:
得:![]()
由余弦定理![]() .
.
由②![]() 及正弦定理,得:
及正弦定理,得:
![]() ,
,
即![]() ,因為
,因為![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
因為![]() 且
且![]() ,
,
所以![]() .所以
.所以![]() ,矛盾.
,矛盾.
所以![]() 不能同時滿足①②.
不能同時滿足①②.
(2)由(1)知,![]() 滿足①③④或②③④
滿足①③④或②③④
若![]() 滿足①③④
滿足①③④
因為![]()
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 的面積
的面積![]()
另:若![]() 滿足②③④
滿足②③④
![]() ,即
,即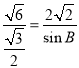 ,則
,則![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的面積
的面積![]() .
.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】冠狀病毒是一個大型病毒家族,已知的有中東呼吸綜合征(MERS)和嚴重急性呼吸綜合征(SARS)等較嚴重的疾病,新型冠狀病毒(nCoV)是以前從未在人體中發現的冠狀病毒新毒株,某小區為進一步做好新型冠狀病毒肺炎疫情知識的教育,在小區內開展“新型冠狀病毒防疫安全公益課”在線學習,在此之后組織了“新型冠狀病毒防疫安全知識競賽”在線活動.已知進入決賽的分別是甲、乙、丙、丁四位業主,決賽后四位業主相應的名次為第1,2,3,4名,該小區為了提高業主們的參與度和重視度,邀請小區內的所有業主在比賽結束前對四位業主的名次進行預測,若預測完全正確將會獲得禮品,現用a,b,c,d表示某業主對甲、乙、丙、丁四位業主的名次做出一種等可能的預測排列,記X=|a﹣1|+|b﹣2|+|c﹣3|+|d﹣4|.
(1)求該業主獲得禮品的概率;
(2)求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直三棱柱ABC﹣A1B1C1,E,F分別是棱CC1,AB的中點.
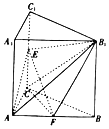
(1)證明:CF∥平面AEB1.
(2)若AC=BC=AA1=4,∠ACB=90°,求三棱錐B1﹣ECF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為2,且過點
的焦距為2,且過點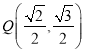 .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
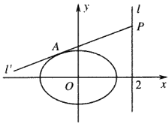
(2)若![]() 為坐標原點,
為坐標原點,![]() 為直線
為直線![]() 上的一動點,過點
上的一動點,過點![]() 作直線
作直線![]() 與橢圓相切于點
與橢圓相切于點![]() ,若
,若![]() 的面積
的面積![]() 為
為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角梯形ABCD中(如圖1),![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點E在CD上,且
,點E在CD上,且![]() ,將
,將![]() 沿AE折起,使得平面
沿AE折起,使得平面![]() 平面ABCE(如圖2),G為AE中點.
平面ABCE(如圖2),G為AE中點.

(Ⅰ)求四棱錐![]() 的體積;
的體積;
(Ⅱ)在線段BD上是否存在點P,使得![]() 平面ADE?若存在,求
平面ADE?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com