
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 根據平面向量的數量積與模長公式,列出方程求出$\overrightarrow{a}$與$\overrightarrow{b}$夾角的余弦值.
解答 解:∵2|$\overrightarrow{a}$|=3|$\overrightarrow{b}$|,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,
∴${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+4${\overrightarrow{b}}^{2}$=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$,
∴2$\overrightarrow{a}$•$\overrightarrow{b}$=${\overrightarrow{b}}^{2}$,
即2|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=${\overrightarrow{b}}^{2}$,
2×$\frac{3}{2}$|$\overrightarrow{b}$|×|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=${|\overrightarrow{b}|}^{2}$;
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{3}$,
即$\overrightarrow{a}$與$\overrightarrow{b}$夾角的余弦值為$\frac{1}{3}$.
故選:C.
點評 本題考查了平面向量的數量積與模長公式的應用問題,是基礎題目.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | 命題“若 x2-5x+6=0,則x=2”的逆否命題是“若 x≠2,則x2-5x+6≠0” | |
| B. | 命題“角α的終邊在第一象限,則α是銳角”的逆命題為真命題 | |
| C. | 已知命題 p和 q,若p∨q 為假命題,則命題 p與q中必一真一假 | |
| D. | 命題“若x>y,則 x>|y|”的逆命題是真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
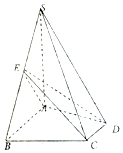 如圖,已知四棱錐S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是邊SB的中點.
如圖,已知四棱錐S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是邊SB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=$\frac{1}{x}$ | B. | y=-x2+1 | C. | y=-e-x-ex | D. | y=sinx |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
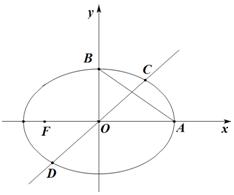 已知橢圓E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,點F、A、B分別為E的左焦點、右頂點,上頂點,|AF|=$\sqrt{2}$+1.
已知橢圓E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,點F、A、B分別為E的左焦點、右頂點,上頂點,|AF|=$\sqrt{2}$+1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com