Question

利用隨機模擬法近似計算圖中陰影部分(曲線y=log₃x與x=3及x軸圍成的圖形)的面積.

Answer 1

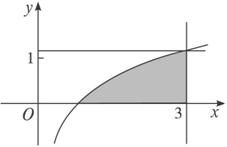
解析：如圖所示,作矩形,設事件A表示“隨機向矩形內投點，所投的點落在陰影部分”.

S1  用計數器n記錄做了多少次投點試驗，用計數器m記錄其中有多少次

（x,y）滿足y＜log₃x(即點落在陰影部分).首先置n=0,m=0;

S2  用變換rand(  )*3產生0—3之間的均勻隨機數x表示所投的點的橫坐標；用函數rand(    )產生0—1之間的均勻隨機數y表示所投的點的縱坐標；

S3  判斷點是否落在陰影部分，即是否滿足y＜log₃x.如果是，則計數器m的值加1，即m=m+1.如果不是，m的值保持不變；

S4  表示隨機試驗次數的計數器n的值加1，即n=n+1.如果還要繼續試驗，則返回步驟S2繼續執行，否則，程序結束.

程序結束后事件A發生的頻率作為事件A的概率的近似值.設陰影部分的面積為S，矩形的面積為3.由幾何概型計算公式得P(A)=.所以≈.所以S≈即為陰影部分面積的近似值.